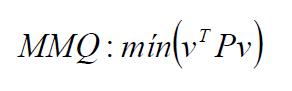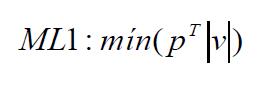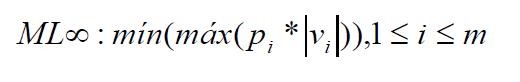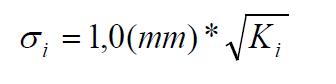Revista Cartográfica 101 | Artículos | ISSN
(impresa) 0080-2085 ISSN (en línea) 2663-3981 julio-diciembre
2020: 135-153
DOI:https://doi.org/10.35424/rcarto.v0i101.669 | Este es un artículo de acceso abierto bajo la licencia CC BY-NC-SA 4.0
Aplicação das normas L1 e L∞ em redes
altimétricas: identificação de outliers
e construção do modelo estocástico
L1
and L∞ norms adjustment in leveling networks:
outlier identification and stochastic modeling
Stefano Sampaio Suraci*
Leonardo Castro
de Oliveira**
Recebido
30 de agosto de 2019; aceito 2 de novembro de 2019
Resumo
Nesse artigo, aplicações
da minimização da norma L1 (ML1) e da norma L∞ (ML∞) na estimação de redes
altimétricas foram investigadas. Redes de nivelamento simuladas pela Técnica de Monte Carlo e dados reais da rede brasileira de nivelamento
foram empregados nos
experimentos. Na identificação
de outliers pela ML1, foi
verificado que o ajustamento com
pesos unitários apresentou condições vantajosas em relação ao modelo estocástico
usual dos pesos proporcionais ao
inverso do comprimento das linhas
de nivelamento. O Classificador
VL1, que estipula um Valor de Corte para os resíduos do ajustamento pela ML1
a partir do qual a respectiva observação
passa a ser classificada
como outlier, foi proposto. A taxa de sucesso dele na identificação de outliers foi superior à do procedimento data
snooping iterativo em cenários
de geometria da rede deficiente. Já
a aplicação da ML∞ investigada é posterior ao tratamento de outliers. Um modelo
estocástico alternativo para ajustamento da rede pelo
MMQ que aproveitou a
característica de minimização do máximo resíduo absoluto da rede no ajustamento
pela ML∞ foi analisado. Além dessa minimização,
o ajustamento da rede pelo MMQ
com o modelo alternativo gerou,
na significativa maioria
dos casos, resíduos e precisão
desses e dos parâmetros
estimados mais homogêneos, com menor desvio padrão, que aqueles com o modelo estocástico usual. Todos os resultados são especialmente relevantes para o caso de redes
altimétricas.
Palavras chaves: normas L1e L∞,
modelo estocástico, Monte Carlo, altimetria.
Abstract
In this paper, applications of L1 norm minimization (ML1) and of L∞ norm minimization (ML∞) in the estimation of leveling networks were investigated. Leveling networks simulated by the Monte Carlo technique and real data from the Brazilian leveling network were employed in the experiments. In the identification of outliers by ML1, it was verified that the adjustment with unit weights presented advantageous conditions in relation to the usual stochastic model of weights of observations as proportional to the inverse of the length of the leveling lines. The Classificador VL1, which stipulates a cut-off value for the residuals of the adjustment by ML1 from which the respective observation is classified as outlier, was proposed. Its success rate in identifying outliers was higher than that of the iterative data snooping procedure in poor network geometry scenarios. The application investigated for ML∞ is after the treatment of outliers. An alternative stochastic model for network adjustment by Least Squares (LS) that took advantage of the characteristic of minimization of the maximum absolute residual of the network in the adjustment by ML∞ was analyzed. In addition to this minimization, the adjustment of the network by LS with the proposed model generated, in most cases, residuals and precision of these and of the estimated parameters more homogeneous, with lower standard deviation, than those with the usual stochastic model. All results are especially relevant for the case of altimetric networks.
Palabras clave: L1 and L∞ norms, stochastic model, Monte Carlo, leveling networks.
Introdução
A altimetria
tem recebido especial atenção atualmente no contexto
dos sistemas de referência. Prova disto é a Resolução 1/2015 (IAG, 2015) da
International Association of Geodesy
(IAG), que definiu o
International Height Reference System
(IHRS), com geoide único e adoção de números geopotenciais, reconhecendo a necessidade de um sistema global de alta acurácia
para investigação de mudanças
na Terra, como a elevação
dos níveis dos oceanos.
Nesse trabalho, aplicações
da minimização das normas L1 e L∞ no contexto da estimação de redes
altimétricas foram investigadas, mais especificamente nas etapas de
identificação de outliers e na definição do modelo estocástico para
ajustamento final da rede pelo Método dos Mínimos Quadrados (MMQ), respectivamente. Com isso, espera-se que seus
resultados contribuam para a definição de metodologias para a implantação de
redes altimétricas a nível nacional e internacional.
Nos subitens
a seguir, a revisão teórica e as situações
específicas que originaram as hipóteses
dessa pesquisa foram
evidenciadas.
Normas L1, L2 e L∞ no
ajustamento de observações
geodésicas
Na estimação de redes
geodésicas, o número de observações é superior ao de incógnitas. Os inevitáveis
erros de medida tornam o sistema inconsistente (Gemael et al., 2015). O ajustamento
da rede é usualmente realizado pelo MMQ, também referenciado por minimização
da norma L2 dos resíduos.
O MMQ minimiza a soma dos quadrados dos resíduos v (diferença
entre valores ajustados e observados), ponderados pela matriz dos pesos das observações P (Equação 1). Seus resultados são os de mínima variância para
os parâmetros estimados e de máxima verossimilhança, essa sob a premissa de ocorrência de somente erros aleatórios normalmente distribuídos
nas observações
(Ghilani, 2010).
|
|
|
|
(1) |
|
|
|
|
|
Apesar de menos conhecida
que o MMQ, a minimização da
norma L1 (ML1) também já foi testada no ajustamento de
redes geodésicas por diversos autores, como (Marshall & Bethel, 1996), (Amiri-Simkooei, 2003) e (Yetkin
& Inal, 2011). Para observações independentes, sendo p o vetor dos pesos, expresso pelos
elementos da diagonal principal de P,
ela minimiza a soma dos resíduos
absolutos ponderados por p (Equação 2). O método SIMPLEx
de programação linear (Dantzig, 1963) é o mais utilizado na literatura
geodésica para solução da ML1.
|
|
(2) |
|
|
|
Outra minimização de norma
vetorial, bem menos explorada na estimação de redes geodésicas, envolve o
ajustamento pela minimização da norma L∞ (ML∞). Por analogia com o caso de
regressão polinomial de (Mason & Handscomb,
2003), o ajustamento pela ML∞ pode ser entendido como a minimização do máximo
resíduo absoluto ponderado pelo peso da respectiva observação (Equação 3),
sendo m o número de observações. (Ebong, 1986) foi o único registro encontrado de aplicação
da norma L∞ em redes geodésicas. Uma formulação detalhada da solução da ML∞ por
programação linear foi apresentada em (Suraci &
Oliveira, 2019a), artigo 1 (de 4) produzido no contexto da dissertação de
mestrado (Suraci, 2018) a que o presente artigo se
refere.
|
|
(3) |
Identificação de outliers em redes geodésicas e a
aplicação da ML1
Apesar de o MMQ ser uma técnica estatística poderosa
para o ajustamento de observações,
ele demanda a inexistência de outliers
para produzir resultados confiáveis
(Yetkin & Inal, 2011). Entretanto, é inviável se garantir a ausência
deles na prática dos levantamentos geodésicos.
Nesse trabalho,
as observações com magnitude do erro total de medida superior a três vezes o seu
respectivo desvio padrão (σ) foram
consideradas outliers. Uma
análise conceitual sobre
termos relacionados a outliers, seus significados e aspectos, foi
apresentada em (Suraci
& Oliveira, 2019b), artigo 2 (de 4) produzido no
contexto da dissertação de mestrado
(Suraci, 2018) a que o presente artigo se refere. Nessas duas referências, essa regra adotada
para definição de outliers
foi intitulada regra
dos 3σ para o erro total.
Há duas principais abordagens para a identificação de outliers
em redes geodésicas: testes estatísticos e métodos
robustos. Classificado no primeiro
grupo, o procedimento data-snooping,
proposto inicialmente por (Baarda,
1968), é um dos melhores
métodos para identificação de outliers
em redes geodésicas (Rofatto et al., 2017). O data-snooping iterativo (Teunissen,
2006), um procedimento que consiste
na aplicação iterativa do data-snooping, é o mais usual e
será referido simplesmente por data-snooping (DS) nesse trabalho. Aplicando o DS, (Rofatto et al., 2018)
apresentaram recentemente uma relevante inovação na identificação de outliers em redes geodésicas: a aferição
de níveis de probabilidade
de acerto e dos diferentes tipos de erro via Simulação de Monte Carlo
(SMC).
A SMC é um tipo de simulação que se baseia em
repetidas amostras aleatórias
das variáveis de entrada, permitindo
dessa forma uma acurada caracterização da variação dos
resultados do modelo a ser estudado (Raychaudhuri, 2008). Quanto maior a quantidade de amostras aleatórias simuladas, mais acurada será a referida caracterização
(Rofatto et al., 2018). Sua
aplicação tem se tornado
usual também na avaliação de métodos de identificação
de outliers em redes geodésicas, podendo ser vista, por exemplo, nesse último artigo, em (Klein et al., 2015), em (Hekimoglu & Erenoglu, 2007) e
em (Durdag et al., 2016).
Já no âmbito
dos métodos robustos, a ML1 também pode ser aplicada na identificação de outliers. Por ser um
método resistente a outliers (Abdelmalek & Malek, 2008), tende
a apresentar resíduos
absolutos relativamente maiores para os outliers das redes analisadas.
Assim, observações com resíduos absolutos
relativamente “grandes” podem ser classificadas
como outliers. Esse procedimento foi demonstrado por (Amiri-Simkooei,
2003) em redes de nivelamento e trilateração,
e por (Yetkin & Inal, 2011) em redes GNSS. Um exemplo
detalhado da questão da classificação de observações como
outlier a partir de seu
resíduo absoluto relativamente “grande” no ajustamento pela ML1 foi apresentado em (Suraci, 2018).
Outras aplicações
da ML1 podem ainda ser
vistas em (Marshall & Bethel, 1996), (Kampmann
& Krause, 1997), (Koch, 1999), (Baselga, 2007), (Khodabandeh & Amiri-Simkooei,
2011), e (Amiri-Simkooei, 2018).
Diversos outros métodos robustos já foram aplicados em redes
geodésicas. Em especial, recentemente, (Koch et al.,
2019) apresentaram aplicações
de alguns deles, com proposta de uma nova
meta-heurística para solução dos mesmos. Vale ressaltar que (Rofatto et al.,
2018) colocam os algoritmos meta-heurísticos, junto com a SMC e os algoritmos genéticos, dentre
outras, como uma das
técnicas cujo potencial ainda
não foi totalmente
explorado em geodésia.
Entretanto, voltando à identificação de outliers
pela ML1, o que seria um resíduo absoluto “grande”? Não há na literatura um critério objetivo estabelecido para classificação
de uma observação como outlier a partir de seu
respectivo resíduo absoluto no ajuste pela ML1. É razoável visualizar que isto se
torna crítico principalmente para outliers de magnitude relativamente menores e para caracterização
de uma rede como sem outlier. O Classificador
VL1 proposto no corrente
artigo estabelece um possível critério a ser adotado.
Ademais, não
há uma investigação
que valide a escolha do resíduo
absoluto como parâmetro de comparação
para identificação de outliers.
Uma vez que o ajustamento
pela ML1 adota determinado modelo estocástico,
pode-se imaginar que o resíduo absoluto ponderado seja também um
parâmetro viável de comparação. Nesse sentido, a
potencial eficácia de um ajustamento com pesos unitários para as observações na identificação de outliers, para o caso do resíduo
absoluto ser mesmo o parâmetro a ser analisado é também passível de investigação.
Essa questão
foi abordada nos experimentos desse
trabalho, sendo intitulada Alternativa
de Pesos e de Parâmetro de Comparação
para a ML1 (APPC-ML1). A verificação da eficácia de se adotar pesos unitários, juntamente com outros aspectos da ML1, foi
abordada em (Suraci et al., 2019), artigo 3
(de 4) produzido no contexto da dissertação
de mestrado (Suraci, 2018)
a que o presente artigo se refere. Em relação a esse último, a
principal contribuição do corrente
artigo corresponde à verificação também
de Alternativa para o Parâmetro de Comparação e sua integração com a Alternativa
de Pesos. Os resultados dessa questão
foram aplicados na construção do Classificador VL1.
Para um apropriado
entendimento dos experimentos, é
importante apresentar ainda
o Método das Equações Medianas (MEM).
Segundo (Hekimoglu et al., 2011), em redes
geodésicas, falhas na identificação de outliers podem ocorrer devido
a pouca redundância das
respectivas observações, independentemente
do método utilizado na identificação
deles. Assim, foi proposto o MEM: um método para identificação de redundância deficiente na geometria de redes geodésicas, que verifica se um conjunto de outliers é controlável (passível de ser confiavelmente identificado) ou não. Maiores detalhes
sobre o MEM no referido artigo.
Modelagem estocástica em redes altimétricas e a aplicação da ML∞
O modelo estocástico
usual em redes altimétricas adota pesos das observações como inversamente proporcionais
ao comprimento das
respectivas linhas de nivelamento.
É baseado em conjecturas
cuja garantia de ocorrência
na prática dos levantamentos é pouco viável, como a utilização de equipamentos com a mesma precisão e adoção da mesma distância em todas as visadas da rede (Ghilani,
2010), o que justifica a busca por abordagens
alternativas para o modelo estocástico de redes altimétricas.
Além disso,
em redes de nivelamento o número de injunções normalmente é relativamente baixo.
No caso da Rede Altimétrica de Alta Precisão (RAAP) do Sistema Geodésico Brasileiro, por exemplo, há apenas uma injunção para o trecho que
atende a maior parte do território.
Com o afastamento das referências de nível (RRNN) da injunção, devido à propagação de covariâncias, isso tende a gerar RRNN
com precisões muito piores do que outras, como visto em (IBGE,
2018).
Da análise da Equação
3, nota-se que, caso se adotem
pesos unitários para as observações,
o ajustamento pela ML∞ irá acarretar a minimização do máximo resíduo
absoluto (MRA) do ajustamento.
No presente trabalho, a abordagem
alternativa para o modelo estocástico do ajustamento
pelo MMQ de redes altimétricas visou
minimizar o MRA desse ajustamento, para verificação dos
possíveis efeitos na homogeneidade dos resultados. Essa investigação foi intitulada Alternativa de Pesos para o MMQ (AP-MMQ).
Deve ficar claro para o leitor que a aplicação da ML∞ é proposta para uma fase posterior
à identificação de outliers
na rede, ou seja, em redes livres de outliers. Isso, também, pois a ML∞ tende a distribuir erros de outliers
entre as demais observações,
o que dificultaria sua aplicação na identificação
dos mesmos (Abdelmalek & Malek, 2008; Suraci & Oliveira, 2019a).
A proposta e a forma de obtenção desse modelo estocástico
alternativo advindo do MRA foram apresentadas em (Suraci & Oliveira, 2019c), artigo 4 (de 4) produzido no contexto da dissertação
de mestrado (Suraci, 2018)
a que o presente artigo se refere. Resumidamente,
para cálculo do mínimo MRA, um
pré-ajuste da rede pela ML∞ com
pesos iguais para as observações
é aplicado. Em seguida, o modelo estocástico alternativo é obtido
iterativamente, incrementando (a cada iteração) o
peso de observações com resíduo absoluto maior que o
mínimo MRA calculado. As iterações
terminam quando nenhum resíduo absoluto dentre as observações da rede for maior que o mínimo MRA, considerando a tolerância
estipulada. Em relação ao
artigo citado, a contribuição do corrente
artigo refere-se à análise
dos resultados do modelo proposto com
aplicação de SMC.
Hipóteses
A partir do conteúdo abordado na introdução, foram formuladas duas hipóteses, a saber:
· Há cenários de redes
altimétricas em que o Classificador VL1 é mais eficaz que o DS na identificação de outliers.
· O ajustamento pelo MMQ de redes altimétricas livres
de outliers com modelagem estocástica advinda do MRA gera resultados mais homogêneos que com o modelo usual.
Metodologia
Conforme visto, as investigações desse trabalho podem ser divididas em três tópicos: a APPC-ML1, o Classificador
VL1 e a AP-MMQ, os quais
são detalhados na sequência.
APPC-ML1
As Alternativas de Pesos
e de Parâmetro de Comparação
para a ML1 foram realizadas de maneira
conjunta nos experimentos, pois se desejou investigar qual abordagem para o modelo estocástico e com
qual parâmetro de comparação, na identificação de outliers
a partir de resultados do ajustamento da rede pela
ML1, apresenta condições mais vantajosas para a execução dessa tarefa. Entendeu-se por vantajosa a ocorrência do parâmetro de comparação do outlier como
sendo o maior dentre as observações da rede.
Caso isto não ocorra, pode-se considerar que houve
o indesejado mascaramento
do outlier.
Nesse trabalho,
com aplicação de SMC, isso foi mensurado em redes
altimétricas pelo percentual de ocorrências
do parâmetro de comparação
do outlier como sendo
o maior dentre as observações da rede (PPCOMR), apresentado na Equação 4. Quanto maior o PPCOMR, mais vantajosa a abordagem conjunta avaliada. Similarmente, para cenários de múltiplos outliers,
o numerador do PPCOMR computou
a quantidade de experimentos em que os valores do parâmetro de comparação dos outliers foram os maiores da rede.
O PPCOMR foi
avaliado também se adotando
pesos unitários com o resíduo absoluto como parâmetro
de comparação e pesos usuais
com o resíduo absoluto
ponderado como parâmetro. Assim,
além da abordagem comum na literatura (pesos usuais com resíduo
absoluto), duas alternativas foram
testadas, totalizando três comparadas. Obviamente, uma quarta opção,
que seria se testar pesos unitários com resíduos absolutos
ponderados, não se fez necessária, pois ela é equivalente à abordagem
alternativa citada de pesos unitários e resíduos absolutos.
O Classificador VL1 proposto
Já foi visto que o ajustamento pela ML1 é resistente a outliers e, assim, normalmente faz com que os resíduos absolutos desses tendam a ser relativamente maiores. Visando tirar proveito dessa característica, a estratégia do Classificador VL1 é determinar um valor de corte (VC), intitulado VCL1, para o resíduo absoluto de uma observação no ajustamento da rede pela ML1, a partir do qual a mesma passará a ser classificada como outlier. Assim, a primeira etapa da aplicação do Classificador é a construção do VCL1 da rede analisada, caso o mesmo não esteja disponível. A Figura 1 ilustra a aplicação completa do Classificador VL1.
Figura 1. Aplicação do Classificador VL1.
Após isso,
a rede deve ser ajustada pela ML1, adotando-se modelo estocástico com
pesos unitários para as observações.
Em seguida, vem a decisão binária sobre a classificação
como outlier de cada observação
da rede, pela comparação de seu
respectivo resíduo absoluto |vi| com o valor de corte VCL1. Caso seja
maior, considera-se que a i-ésima observação é um outlier (Equação 5).
Vale esclarecer que a decisão de se utilizar a ML1 com pesos unitários e a confirmação do resíduo absoluto como parâmetro
de comparação para o Classificador
VL1 está amparada pelos resultados dos experimentos da APPC-ML1, que são apresentados na sequência desse
artigo. Neles se verificou que com
essa abordagem conjunta houve maior PPCOMR.
Para construção do valor de corte VCL1 do Classificador
VL1 (Figura 2), cenários aleatórios
com outlier
referentes à rede altimétrica analisada devem ser preparados via SMC. Concluídas as simulações, um VCk é estipulado - k é o número de ordem
do VC. Fazendo VCL1 = VCk, testa-se o comportamento dele para todos os cenários
simulados da rede analisada, obtendo-se
a respectiva Taxa de Sucesso (TS) (Equação
6). Esse processo é
iterativo até que se chegue, por tentativa e erro, a um VCk
no qual a TS seja máxima, o qual será o valor
final para o VCL1 a ser empregado para a identificação de
outliers.
Figura 2. Diagrama de atividades para construção do VCL1.
A aplicação do Classificador VL1 na identificação de outliers foi avaliada por comparação com o DS, em relação
a cenários de redes nos quais
os outliers eram conhecidos. A comparação entre os
métodos, em ambos os casos, foi feita
pelas respectivas TS.
AP-MMQ
Seja |v| o vetor
do valor absoluto dos resíduos, e Ex e Ev o das raízes
quadradas dos elementos da diagonal principal das MVCs (que representam as precisões) dos parâmetros
estimados e dos resíduos no ajustamento
pelo MMQ, respectivamente. Via
SMC, para verificação da homogeneidade
dos resultados, os desvios padrão
dos elementos dos vetores |v|, Ex e Ev, após ajustamento das redes sem outliers
pelo MMQ com o modelo
estocástico usual dos pesos proporcionais ao inverso do comprimento das linhas de nivelamento, e com o modelo estocástico alternativo advindo
do MRA, foram comparados.
Dados
Para consecução dos
experimentos, observações reais
da RAAP e cenários obtidos por SMC a partir de uma
rede matemática foram utilizados.
Rede Matemática –
base para SMC
As observações da
rede matematicamente “perfeita” correspondem propositalmente aos desníveis
exatos entre as respectivas RRNN. Trata-se de uma
rede sem qualquer erro de medida (nem mesmo aleatórios), útil para aplicação de
SMC, assim como feito por (Hekimoglu
& Erenoglu, 2007). Nas simulações a partir dela,
a altitude do ponto A é considerada fixa e com valor hA=0.
Assim, foram simuladas redes com 20 observações e 10 pontos de altitudes a
determinar (incógnitas), ou seja, 10 graus de liberdade. A geometria das redes
simuladas consta da Figura 3.
Figura
3. Geometria da rede
matemática e das simulações decorrentes.
Foi intitulada Simulação 1 a criação, a partir da Rede Matemática, de cenários aleatórios de rede
altimétrica sem outliers. As observações
foram simuladas da mesma forma que as “observations without outliers” do caso de heterocedasticidade
de (Hekimoglu & Erenoglu,
2007), com apenas uma diferença: como no corrente
artigo se adotou a regra dos 3σ para o erro total (Suraci & Oliveira, 2019b) na definição de outlier, valores de erro aleatório
com magnitude superior aos 3σ
não foram considerados. Nas simulações a partir da Rede
Matemática, o desvio padrão
das observações foi dado
pela Equação 7, sendo K (em
km) o comprimento da respectiva linha.
|
|
(7) |
Já a Simulação 2 correspondeu
à criação, a partir da Rede Matemática, de cenários aleatórios de rede
altimétrica com outliers. As “boas” observações foram simuladas assim como na Simulação
1, e a simulação de outliers foi
inspirada na das “bad observations” com sinal aleatório de (Hekimoglu & Erenoglu, 2007). Maiores detalhes em (Suraci, 2018).
Rede real – trecho da RAAP
Os dados da RAAP
utilizados nos experimentos foram adaptados de (Beserra, 1952). Tratam-se dos
dados do nivelamento geométrico de precisão do território brasileiro
que tinha sido realizado até então,
configurando 105 linhas de nivelamento
(observações), com um comprimento total de 15.706,25
km, passando por diversos estados do território brasileiro. O retângulo
envolvente correspondente a este nivelamento
é apresentado na Figura 4. Um arquivo nomeado
“Rede_real_geometria.pdf” e um nomeado
“Rede_real_observacoes.pdf”, nos quais a geometria, e os comprimentos e desníveis das observações dessa rede podem ser vistos com maior detalhamento,
foram disponibilizados em (Suraci, 2019).
A altitude de uma das RRNN (da RRNN chamada 3L) foi considerada fixa (injunção fixa) e com valor h3L=10,8190m. Com
uma quantidade de pontos de
altitude a determinar de 67, o número de graus de liberdade é 38. Não foram identificados outliers nessa rede pelo DS (com α=0,001),
adotando-se pesos das observações
equivalentes ao inverso do comprimento
das respectivas linhas, multiplicados por um fator de proporcionalidade
A=200, como feito por (Beserra,
1952).
Descrição dos experimentos e Resultados
Os experimentos foram conduzidos no software Octave.
As soluções dos ajustamentos pelas normas L1 e L∞ foram feitas por programação
linear, utilizando o método
Figura
4. Retângulo envolvente da rede
real.
SIMPLEx. O estado inicial das sequências de números pseudoaleatórios foi
modificado sempre que necessário para evitar qualquer viés nos resultados. Os
códigos dos experimentos estão disponibilizados em (Suraci,
2019).
Experimento 1 –
APPC-ML1
No Experimento 1, a APPC-ML1
foi testada em cenários de
rede obtidos pela Simulação
2. A Tabela 1 apresenta
o PPCOMR (Equação 4) para
diferentes intervalos de magnitude do erro do outlier propositalmente
inserido. A linha “PIV”
corresponde aos resultados dos ajustamentos
pela ML1 com pesos pelo inverso da variância das respectivas observações
(logo, proporcionais ao
inverso do comprimento das linhas
de nivelamento – Equação 7)
e a “PUnit” com pesos unitários para as observações da
rede. Já os parâmetros de comparação são indicados por “RA”
para o resíduo absoluto e “RAP” para o resíduo absoluto ponderado. O total de cenários
de rede simulados, para cada intervalo de magnitude
de erro total inserido, foi de 200.000.
Tabela 1
PPCOMR – cenários com 1 outlier – Experimento 1
|
Erro Total |
3-6σ |
6-12σ |
12-25σ |
25-100σ |
|
|
PUnit |
RA |
63,79% |
95,01% |
99,92% |
100,00% |
|
PIV |
RA |
58,10% |
84,32% |
89,88% |
90,07% |
|
PIV |
RAP |
59,29% |
86,65% |
90,05% |
90,07% |
A Tabela 2 é similar à
Tabela 1, mas para o caso de 2 outliers em cada cenário de rede
simulado.
Tabela 2
PPCOMR – cenários com 2 outliers –
Experimento 1
|
Erro Total |
3-6σ |
6-12σ |
12-25σ |
25-100σ |
|
|
PUnit |
RA |
38,02% |
79,76% |
89,37% |
89,66% |
|
PIV |
RA |
32,06% |
62,92% |
71,03% |
71,37% |
|
PIV |
RAP |
33,13% |
65,64% |
71,29% |
71,37% |
Da análise das Tabelas
1 e 2, nota-se que o PPCOMR
foi sempre maior no ajustamento pela ML1 com pesos unitários. Assim, verifica-se que a adoção de pesos unitários para as
observações no ajustamento
pela ML1 apresentou condições
vantajosas para a identificação
de outliers em relação
aos usuais pesos proporcionais ao inverso do comprimento das linhas de nivelamento.
Vale notar ainda que a utilização de pesos usuais com o resíduo absoluto como parâmetro de comparação, abordagem conjunta comum na literatura, apresentou em geral o pior resultado (menor PPCOMR) dentre as três avaliadas. Ademais, as três abordagens conjuntas obtiveram aumento do PPCOMR para maiores magnitudes dos outliers
inseridos e diminuição do PPCOMR
com o aumento da quantidade
de outliers.
Experimento 2 – Classificador VL1 proposto
O Experimento 2 visou comparar o desempenho do Classificador VL1 com o do DS na identificação
de outliers. Para construção
do VCL1, foram
utilizados cenários de rede com
1 outlier (com magnitude entre 3σ e 100σ) obtidos
pela Simulação 2. De um total de 200.000 cenários
simulados na identificação
de outliers para cada um
dos diversos VCs testados, o valor de 29,2 mm foi selecionado, por ter obtido a maior quantidade de acertos (191.307).
Para cada cenário, foi
considerado que houve acerto
se o outlier foi
identificado, sem que nenhuma
outra observação também tenha sido assim classificada.
Deve-se atentar para o fato de que a construção do VCL1
ora apresentada foi feita com inserção
de outliers entre 3σ e 100σ, nos moldes da Simulação 2. A construção do VCL1 com inserção proposital de outliers com outros intervalos de magnitude, o
que ocasionou diferentes valores para o VCL1 e, em consequência,
diferentes TSs (Equação 6)
para o Classificador VL1 nos experimentos a seguir, foi vista em (Suraci, 2018).
Na continuidade,
o Classificador VL1, com o VCL1 construído,
foi aplicado em cenários de
rede com as diferentes magnitudes de erro dos outliers da Tabela 3, obtidos via Simulação
2. Para cada faixa de magnitude
de outlier, foram
testados 200.000 cenários simulados. A Tabela 3 apresenta a TS do Classificador VL1 e do DS nesse contexto.
Tabela 3
TS – 1 outlier – Experimento 2
|
Método |
3-6σ |
6-12σ |
12-25σ |
25-100σ |
|
DS
(α=0,001) |
42,90% |
93,92% |
98,75% |
98,76% |
|
Classificador VL1 |
18,99% |
79,02% |
98,93% |
99,11% |
A Tabela 4 é similar à
Tabela 3, mas para o caso de 2 outliers inseridos propositalmente em
cada cenário de rede simulado via Simulação 2. Nesse contexto, foi considerado
que houve acerto na identificação de outliers se ambos foram
identificados pelo método aplicado, sem que nenhuma outra observação também
tenha sido assim classificada.
Tabela 4
TS – 2 outliers – Experimento 2
|
Método |
3-6σ |
6-12σ |
12-25σ |
25-100σ |
|
DS
(α=0,001) |
14,32% |
76,55% |
87,29% |
88,88% |
|
Classificador VL1 |
3,35% |
56,34% |
87,90% |
88,32% |
No caso anterior de 1 outlier,
o DS apresentou tempo médio computacional inferior ao
do Classificador VL1 (os tempos foram
de 2,6 ms e 2,9 ms, respectivamente). Porém, seguindo para os testes com 2 outliers, o tempo médio do
Classificador VL1 se manteve
estável (2,9 ms), enquanto
o do DS (4,2 ms) obteve uma tendência de crescimento, passando a ser maior que o do Classificador VL1.
Isso era esperado, pois o DS é um método iterativo, enquanto o Classificador VL1
identifica os outliers em uma
única iteração.
As Tabelas 5 e 6 são
similares à Tabela 4, mas
tratando separadamente os casos de 2 outliers controláveis e de 2 não controláveis (considerando a análise
da geometria da rede pelo MEM),
respectivamente. Para o primeiro caso, a TS do DS foi
sempre superior à do Classificador
VL1. Entretanto, se ressalta o resultado do Classificador VL1 em cenários de dois outliers não controláveis,
significativamente superior ao do DS.
Tabela 5
TS – 2 outliers controláveis –
Experimento 2
|
Método |
3-6σ |
6-12σ |
12-25σ |
25-100σ |
|
DS
(α=0,001) |
16,01% |
84,75% |
95,99% |
97,23% |
|
Classificador VL1 |
3,46% |
59,19% |
93,48% |
93,94% |
Tabela 6
TS – 2 outliers não
controláveis – Experimento 2
|
Método |
3-6σ |
6-12σ |
12-25σ |
25-100σ |
|
DS
(α=0,001) |
1,24% |
19,39% |
27,07% |
31,36% |
|
Classificador VL1 |
2,03% |
34,56% |
49,59% |
49,71% |
Contudo, é lícito afirmar
que o Experimento 2 mostrou que há cenários de redes altimétricas em que o
Classificador VL1 foi mais eficaz que o DS na
identificação de outliers, especialmente no caso de geometria da rede
deficiente.
Experimento 3 – AP-MMQ
No Experimento 3, primeiramente a AP-MMQ foi
testada em 2.000 cenários de rede obtidos pela Simulação 1. O MRA médio calculado no ajustamento pela ML∞ dos cenários
simulados foi de 6,2162 mm. O modelo estocástico alternativo foi obtido, em
média, após 34 iterações do ajustamento pelo MMQ.
A Tabela 7 apresenta a
quantidade de cenários nos quais o desvio padrão (σ) dos elementos de |v|, Ev e Ex foi menor (caracterizando
maior homogeneidade dos elementos) para os ajustamentos pelo MMQ com modelo estocástico usual (ME usual) e com o modelo
estocástico alternativo (ME alternativo) advindo do MRA.
Tabela 7
Quantidade
de resultados mais homogêneos – Experimento 3 – Simulação 1
|
σ |
ME usual |
ME alternativo |
|
|v| |
35 |
1965 |
|
Ev |
153 |
1848 |
|
Ex |
241 |
1759 |
Em seguida, a AP-MMQ foi testada na Rede Real com dados da RAAP. A Tabela 8 apresenta os valores do desvio padrão dos
elementos de |v|, DPv e DPx para os
ajustamentos pelo MMQ com o ME usual e com o ME
alternativo. O MRA calculado no ajustamento pela ML∞
para a rede foi de 0,1392 m. O modelo estocástico alternativo foi obtido após
15 iterações. Vale esclarecer que o ajustamento pelo MMQ
com o ME alternativo apresentou MRA (máximo elemento
de |v|) inferior em todos os casos
(2.000 cenários simulados e rede com dados da RAAP).
Obviamente, isso era de se esperar, pois esse modelo estocástico foi construído
de forma a implicar isso.
Tabela 8
Resultados
do ajustamento pelo MMQ – Experimento 3 – Trecho da RAAP
|
σ |
ME usual |
ME alternativo |
|
|v| |
0,0281 m |
0,0238 m |
|
Ev |
0,0178 m |
0,0042 m |
|
Ex |
0,0248 m |
0,0225 m |
Da análise da Tabela
7, verifica-se que o desvio
padrão dos elementos dos vetores
|v|, DPv e DPx com
o ME alternativo foi menor que os equivalentes com o ME usual em cerca de 98%, 92% e 88% dos cenários simulados, respectivamente. Essa
tendência também foi vista com os dados reais da RAAP (Tabela 8). Assim, na significativa maioria dos cenários analisados, o ajustamento pelo MMQ de redes
altimétricas livres de outliers
com modelagem estocástica
alternativa advinda do MRA gerou resultados mais homogêneos que com o modelo
usual.
A desvantagem do ME alternativo é que
esta ponderação dificilmente
reflete a realidade da rede. Neste
caso o ajustamento das observações
é obtido única e exclusivamente em função dos dados de campo e da configuração
geométrica da rede. Logo, os resultados obtidos não necessariamente conduzem a uma solução ótima, uma vez que o modelo estocástico foi
simplificado. Apesar do ME usual também
representar uma simplificação,
espera-se que ele seja uma aproximação
mais realista.
Por fim, diante
dos resultados, não se pode indicar qual dos modelos estocásticos deve
ser seguido. Um modelo não exclui o outro. Contudo, os promissores
resultados com o ME alternativo advindo
do MRA mostram haver indícios da possibilidade de maiores investigações sobre o mesmo, ou
até de formas de combinar os dois modelos
estocásticos, visando resultados mais realistas e apropriados.
Conclusões e implicações para a
prática da estimação de
redes altimétricas
O Classificador
VL1 proposto apresentou TS significativamente superior à do DS
em cenários de outliers
não controláveis
(considerando o MEM). Isso
é particularmente relevante para redes com grande quantidade de observações, mas baixa redundância
função da geometria mais pobre, caso da RAAP e das
redes de nivelamento de forma geral.
A implantação de extensas redes altimétricas com geometria que permita grande resistência contra múltiplos outliers
possui custo elevado, de
forma que métodos com maior
eficácia em cenários de
menor resistência são de
grande valia.
O tempo de execução computacional do Classificador VL1 se mantém estável com o aumento da quantidade de outliers nas observações, enquanto o do DS tende a ser aumentado, por ser esse
último um método iterativo. Isso
representa também uma vantagem do Classificador VL1
para cenários com quantidade relativamente grande de observações,
como redes de nivelamento a nível
nacional.
Quanto à aplicação
da norma L∞, o modelo estocástico alternativo gerou resíduos e precisão desses e dos parâmetros estimados
mais homogêneos, com menor desvio padrão, que aqueles com a abordagem usual para o
modelo estocástico, na significativa maioria dos casos analisados. Isso pode ser aproveitado para
que se evitem redes com vértices
relativamente muito menos precisos que outros, especialmente quando o
controle é baixo, algo também
comum em redes de nivelamento.
Este artigo é apresentado a partir dos
resultados da Dissertação de Mestrado intitulada: “Aplicação das normas L1 e L∞
em redes altimétricas: identificação de outliers
e construção do modelo estocástico”, defendida em 19 de dezembro de 2018.
Bibliografia
Abdelmalek, N. & Malek, W. (2008). Numerical linear approximation in C. CRC Press: Boca Raton, EUA,
Taylor & Francis Group.
Amiri-Simkooei, A. (2003). “Formulation of L1 Norm Minimization in Gauss-Markov
Models”, Journal of Surveying
Engineering, fev., pp. 37-43. https://doi.org/10.1061/(ASCE)0733-9453(2003)129:1(37)
Amiri-Simkooei, A. (2018). “On the use of two L1 norm minimization methods in geodetic
networks”, Earth Observation and Geomatics Engineering, 2(1): 1-8. https://doi.org/10.22059/EOGE.2018.256034.1021
Baarda,
W. (1968). “A testing procedure for use in geodetic networks”, Publications on Geodesy - New Series,
2(5): 1-97. Disponível em http://www.ncgeo.nl/downloads/09Baarda.pdf
Baselga, S. (2007). “Global Optimization Solution of Robust
Estimation”, Journal of Surveying Engineering, 133(3): 123-128.
https://doi.org/ 10.1061/(ASCE)0733-9453(2007)133:3(123)
Beserra, H. (1952). Ajustamento da rede de nivelamento, IBGE, Rio de Janeiro, Brasil, Biblioteca Geográfica Brasileira.
Dantzig, G.
(1963). Linear Programming and Extensions,
The Rand Corporation, Santa Monica, EUA, Princeton
University Press.
Durdag,
U.M., Hekimoglu, S. & Erdogan, B. (2016).
“Outlier detection by using fault detection and isolation techniques in
geodetic networks”, Survey Review, 48(351): 400-408. https://doi.org/10.1179/1752270615Y.0000000038
Ebong, M.B. (1986). “The Chebyshev adjustment of a geodetic levelling network”, Survey Review, 28(220): p. 315-321. https://doi.org/10.1179/sre.1986.28.220.315
Gemael, C., Machado, A.M.L. & Wandresen, R. (2015). Introdução ao
ajustamento de observações: aplicações geodésicas, (2). UFPR, Curitiba, Brasil,
Ed. UFPR.
Ghilani,
C. (2010). Adjustment Computations:
Spatial Data Analysis, (5), John Wiley & Sons, Hoboken, EUA.
Hekimoglu,
S., Erenoglu, R.C., Sanli, D.U. & Erdogan, B.
(2011). “Detecting
Configuration Weaknesses in Geodetic Networks”, Survey Review, 43(323): 713-730. https://doi.org/10.1179/003962611X13117748892632
Hekimoglu,
S. & Erenoglu, R.C.
(2007). “Effect of heteroscedasticity
and heterogeneousness on outlier detection for geodetic networks”, Journal of Geodesy, 81: 137-148. https://doi.org/10.1007/s00190-006-0095-z
IAG
(2015). IAG Resolution (No. 1/2015) for the definition
and realization of an International Height Reference System. Disponível em https://ihrs.dgfi.tum.de/fileadmin/JWG_2011/IAG_Resolutions_2015.pdf
IBGE (2018). Reajustamento da Rede Altimétrica com
Números Geopotenciais 2018, IBGE, Rio de Janeiro,
Brasil. Disponível em https://biblioteca.ibge.gov.br/visualizacao/livros/liv101666.pdf
Kampmann,
G. & Krause, B. (1997). “A breakdown point analysis for the straight line
fit based on balanced observations”, Bollettino di Geodesia e Scienze Affini, 3: 293-303.
Khodabandeh, A. & Amiri-Simkooei, A. (2011). “Recursive Algorithm for L1 Norm
Estimation in Linear Models”, Journal of Surveying Engineering,
137(1): 1-8. https://doi.org/10.1061/(ASCE)SU.1943-5428.0000031
Klein, I.,
Matsuoka, M.T., Guzatto, M.P., Souza, S.F. & Veronez, M.R., (2015). “On evaluation of different methods
for quality control of correlated observations”, Survey review, 47(340): 28-35.
https://doi.org/10.1179/1752270614Y.0000000089
Koch, I.E.,
Klein, I., Gonzaga Jr., L., Matsuoka, M.T., Rofatto,
V.F., Veronez, M.R. (2019). “Robust Estimators in
Geodetic Networks Based ona New Metaheuristic:
Independent Vortices Search”, Sensors, 19(20),
4535, pp. 1-27. https://doi.org/10.3390/s19204535
Koch, K.
(1999). Parameter Estimation and Hypothesis Testing in Linear Models, (2), Springer, Berlim,
Alemanha.
Marshall, J.
& Bethel, J. (1996). Basic concepts of L1 norm minimization for surveying
applications, Journal of Surveying
Engineering, 122(4): 168-179. https://doi.org/10.1061/(ASCE)0733-9453(1996)122:4(168)
Mason, J.C.
& Handscomb, D.C., Chebyshev polynomials, CRC Press, Florida, EUA,
2003.
Raychaudhuri,
S. (2008). “Introduction to Monte Carlo Simulation”, Proceedings of the 2008 Winter Simulation Conference, pp. 91-100. Disponível em https://dl.acm.org/citation.cfm?id=1516768
Rofatto,
V., Matsuoka, M. & Klein, I. (2017). An Attempt to Analyse
Baarda’s Iterative Data Snooping Procedure based on
Monte Carlo Simulation. South African
Journal of Geomatics, 6(3): 416-435. Disponível em http://www.sajg.org.za/index.php/sajg/article/view/578
Rofatto,
V.F., Matsuoka, M.T., Klein, I., Veronez, M.R., Bonimani, M.L. & Lehmann, R.
(2018). “A half-century of Baarda’s concept of
reliability: a review, new perspectives, and applications”, Survey Review, https://doi.org/10.1080/00396265.2018.1548118
Suraci, S.S. (2018). Aplicação das normas L1 e L∞ em redes altimétricas: identificação de outliers e construção do modelo estocástico, Dissertação Mestrado em Engenharia Cartográfica, IME: Rio de Janeiro, Brasil. Disponível em https://1drv.ms/b/s!AlQm3WMI4DY1gdNKKtQ5NTnu7PQUQg
——— (2019). “GitHub
de Stefano Sampaio Suraci”, Disponível em https://github.com/stefano998/artigoRevCartografica
Suraci,
S.S. & Oliveira, L.C. (2019a). “Chebyshev norm minimization: what to expect? Case study in a leveling network”, Revista
Brasileira de Geomática: no prelo.
——— (2019b). “Outlier=gross error? Do only Gross errors cause
outliers in geodetic networks? Addressing these and other questions”,
Boletim de Ciências Geodésicas, 25: 1-16.
https://doi.org/10.1590/s1982-21702019000s00004
——— (2019c). “Proposta de modelo estocástico para minimização do máximo
resíduo absoluto em redes de nivelamento”, Revista
Militar de Ciência e Tecnologia, 36: 55-58. Disponível em http://ebrevistas.eb.mil.br/index.php/CT/article/view/2722
Suraci,
S.S., Oliveira, L.C. & Klein, I., (2019). “Two aspects on L1-norm adjustment of leveling
networks”, Revista Brasileira de Cartografia, 71(2):
486-500. https://doi.org/10.14393/rbcv71n2-47697
Teunissen,
P., (2006). Testing theory: an introduction,
(2), Delft Univ. of Technology: Delft, Holanda.
Yetkin, M. & Inal, C. (2011). L1 norm minimization in GPS networks. Survey Review, 43(323): 523-532. https://doi.org/10.1179/003962611X13117748892038