Revista Cartográfica 101 | Artículos | ISSN
(impresa) 0080-2085 ISSN (en línea) 2663-3981 julio-diciembre 2020: 71-97
DOI: https://doi.org/10.35424/rcarto.v0i101.689 | Este es un artículo de acceso abierto bajo la licencia CC BY-NC-SA 4.0
Un
modelo de mareas para el
Observatorio Argentino-Alemán de Geodesia (AGGO), utilizando observaciones
del gravímetro superconductor SG038
A tidal model for the
Argentinean-German Geodetic
Observatory (AGGO) by using superconducting
gravity observations of SG038
Ezequiel Darío Antokoletz*
Claudia Noemí Tocho**
Hartmut Wziontek***
Recibido 18 de febrero 2020; aceptado 29 de mayo 2020
Resumen
El
Observatorio Argentino-Alemán de Geodesia (AGGO) es un observatorio fundamental
de geodesia ubicado en las cercanías de la ciudad de La Plata, Argentina. AGGO
cuenta con las principales técnicas geodésicas espaciales, GNSS, VLBI y SLR.
Por otra parte, AGGO posee un Laboratorio de Gravimetría, donde el gravímetro
superconductor (SG) SG038 realiza mediciones en forma continua de las
variaciones de gravedad, desde diciembre del año 2015. Además, el gravímetro
absoluto FG5-227 provee un valor de gravedad absoluto de referencia para AGGO y
para Latinoamérica desde enero del año 2018. En este trabajo se presenta un modelo
de mareas obtenido a partir del análisis de tres años de observaciones del SG.
Los SGs son capaces de medir variaciones de la gravedad en un gran espectro de
amplitudes y frecuencias, desde mareas terrestres hasta efectos hidrológicos.
Para analizar distintos efectos en las observaciones de un SG, primero debe
realizarse un cuidadoso tratamiento de la señal observada. Para esto se
obtuvieron los residuos preliminares, luego de eliminar las principales fuentes
de variaciones de gravedad. Saltos y picos ocasionados por terremotos, cortes
de luz, etc., fueron eliminados de la señal residual y a su vez filtrada,
obteniendo una señal suave y continua. Luego, las señales de mareas terrestres
y carga oceánica fueron restituidas a la señal residual. El procesamiento de la
señal resultante se realizó con la última versión del software ETERNA ETA34-X,
incluyendo el grado 3 del potencial de marea de ciertas ondas de marea en el
análisis de marea. Como resultado del análisis de tres años de observaciones,
se obtuvieron los parámetros de marea de 55 grupos de onda. En segundo lugar,
se ha analizado el impacto de distintos modelos de marea oceánica en los parámetros,
con el fin de separar los efectos de marea terrestre y carga oceánica.
Palabras clave: gravímetro
superconductor, Observatorio Argentino-Alemán de Geodesia, parámetros de marea.
Abstract
The Argentinean-German Geodetic Observatory (AGGO) is
a fundamental geodetic observatory located close to the city of La Plata,
Argentina. All relevant space geodetic techniques are established at AGGO:
GNSS, VLBI and SLR. A Gravity Lab is also installed, where the superconducting
gravimeter (SG) SG038 has been continuously measuring gravity variations since
December 2015. Moreover, the absolute gravimeter FG5-227 has provided a gravity
reference value for the Observatory and Latin America since January 2018.
Through the analysis of three years of superconducting gravity data, an Earth
tidal model is presented. The SGs are capable to measure gravity variations in
a wide range of amplitudes and frequencies, from Earth tides to hydrological
effects. In order to analyse different effects in the SG observations, a careful
pre-processing of the signal has to be done before. To do so, the preliminary
residuals were obtained by subtracting the principal constituents of the
signal. Spikes caused by earthquakes were eliminated and a few gaps were
filled. The residuals were then filtered to obtain a smooth and continuous
signal. Afterwards, Earth tides and ocean tide loading signals that were
previously subtracted, were restored to the corrected residuals. The tidal
analysis was performed with the last version of the ETERNA ETA34-X software,
including independent estimates of degree 3 of the potential of some tidal
constituents. After the tidal analysis of three years of SG observations,
parameters of 55 tidal constituents were obtained. Moreover, in order to
separate the effects of Earth tides and ocean tide loading, different ocean
tide models were compared.
Key words: Superconducting gravimeter,
Argentinean-German Geodetic Observatory, Tidal parameters.
Introducción
El Observatorio Argentino-Alemán de Geodesia (AGGO)[1] es un observatorio fundamental de geodesia ubicado en el Parque Pereyra Iraola, en las cercanías de la ciudad de La Plata, Argentina (Figura 1). El mismo surge como un proyecto conjunto entre la Agencia Federal para la Cartografía y la Geodesia (BKG)[2] de Alemania y el Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) de Argentina. AGGO cuenta con las principales técnicas geodésicas espaciales: interferometría de base muy larga (VLBI)[3], láser a satélite (SLR)[4] y sistemas de navegación por satélite (GNSS)[5]. Por otra parte, AGGO cuenta con un laboratorio de gravimetría donde un gravímetro superconductor (SG) es operado en forma continua desde el 16 diciembre del año 2015, y un gravímetro absoluto (AG) realiza determinaciones de gravedad absoluta desde enero del año 2018. El patrón de tiempo y frecuencia del observatorio se mantiene a través de relojes atómicos, un máser de hidrógeno y dos de cesio.
Como mediciones complementarias, AGGO cuenta con una estación meteorológica con sensores de precipitación, presión atmosférica, humedad, dirección y velocidad del viento y radiación solar. Además, sensores hidrológicos fueron instalados en cooperación con el Centro Alemán de Investigación en Geociencias (GFZ).[6]
Anteriormente,
los instrumentos formaban parte del Observatorio Geodésico Integrado
Transportable (TIGO)[7]
instalado en los alrededores de la ciudad de Concepción, Chile (Hase et al.,
2003). En abril del año 2015, luego de un traslado por tierra de más de 3 000
kilómetros, AGGO se establece como el único observatorio geodésico con estas
características en América del Sur y el Caribe. Las coordenadas geodésicas de
AGGO en el marco de referencia POSGAR07 época 2006.632 (Cimbaro et al.,
2009) son: Latitud = -34º 52’ 25.34914’’, Longitud = -58º 08’ 23.48308’’ y
Altura elipsoidal = 23.505 m.
Las distintas técnicas geodésicas establecidas en AGGO contribuyen a servicios internacionales, dependientes de la Asociación Internacional de Geodesia (IAG):[8]
· VLBI contribuye al Servicio Internacional de VLBI (IVS).[9]
· SLR contribuye al Servicio Internacional de Rastreo Láser (ILRS).[10]
· GNSS contribuye al Servicio Internacional de GNSS (IGS).[11]
Por otra parte, el gravímetro superconductor SG038 instalado en AGGO contribuye al Servicio Internacional de Geodinámica y Mareas Terrestres (IGETS,[12] Voigt et al., 2016; Wziontek et al., 2017). El IGETS se estableció en el año 2015 como una continuación del Proyecto Global para la Geodinámica (GGP).[13] Es un servicio de la IAG, y es coordinado por el Servicio Internacional del Campo de Gravedad (IGFS).[14] El IGETS es el responsable de recolectar y distribuir mediciones continuas del campo de gravedad realizadas con gravímetros en la superficie terrestre. El objetivo principal de este servicio es el de monitorear variaciones temporales del campo de gravedad de la Tierra y deformaciones en su superficie. El gravímetro absoluto FG5-227 instalado en AGGO provee a AGGO con mediciones absolutas de la gravedad, las cuales contribuyen a la Base de Datos de Gravedad Absoluta (AGrav;[15] Wziontek et al., 2012), mantenida conjuntamente por la BKG y el Servicio Internacional de Gravedad (BGI).[16]
Una de las principales fuentes de variaciones temporales en las mediciones realizadas con gravímetros son las mareas terrestres y oceánicas. Éste es un efecto periódico generado por la atracción gravitatoria de los cuerpos celestes que rodean a la Tierra. Los efectos más importantes se deben a la atracción que generan la Luna y el Sol. En forma similar, el resto de los cuerpos celestes (planetas) generan un efecto sobre la Tierra, aunque el mismo es considerablemente menor en comparación a los producidos por la Luna y el Sol. Además de la atracción, este efecto genera variaciones en la distribución de masas en el interior de la Tierra y desplazamientos en su superficie.
El análisis de las series de tiempo observadas con gravímetros permite conocer cómo la Tierra es deformada por el efecto de mareas y establecer parámetros con el fin de predecir dicho efecto a lo largo del tiempo. En el presente trabajo se realiza una revisión de los conceptos referidos al potencial generador de mareas, las mareas terrestres y el fenómeno de carga oceánica. Además, se abordan los conceptos relacionados al análisis de marea y a las ecuaciones involucradas en el ajuste por mínimos cuadrados de los parámetros de marea. En una segunda sección, se presenta la metodología aplicada para realizar el pre-procesamiento de las observaciones y el análisis de marea. Para el presente trabajo se ha tenido en cuenta la serie de tres años (2016 al 2018) observada por el gravímetro superconductor SG038 instalado en AGGO. Por último, se realiza un análisis de los resultados, comparados con los obtenidos a partir de un modelo de Tierra y diferentes modelos de carga oceánica.
b)
Figura 1. a) Red de estaciones del IGETS y b) ubicación de AGGO.
Marco teórico
A continuación, se desarrollan los conceptos que permiten analizar las fuerzas que dan origen al fenómeno de mareas. En segundo lugar, se describe cómo la Tierra responde a las fuerzas de marea, dando lugar a la señal de marea observada. Por último, se describen las ecuaciones involucradas en el análisis de marea.
Fuerza, potencial y
aceleraciones de marea para una Tierra rígida
En un sistema de dos cuerpos (Figura 2), además de la fuerza gravitacional ejercida por el cuerpo a cada punto de la Tierra, existe una fuerza de carácter centrífugo generada por el hecho de que ambos cuerpos giran en torno al centro de masas del sistema (en el caso Tierra-Luna, el centro de masas se encuentra dentro del núcleo terrestre, muy cercano al centro de masas de la Tierra). Debido a la naturaleza de esta fuerza, ésta afecta de igual manera en todos los puntos de la Tierra.
Figura 2. Fuerzas actuantes en un sistema de dos cuerpos.
De esta manera, la fuerza de mareas se define como la suma de estas dos fuerzas (Furones et al., 2003):
|
|
(1) |
donde:
-
-
Dicho campo de fuerzas puede analizarse en
términos de una aceleración de
mareas:
|
<
|
(2) |
|
|
|
donde:
-
-
-
<
-
Al igual que la aceleración de la gravedad
de la Tierra, es posible obtener la aceleración de marea a partir de un
potencial armónico, llamado potencial generador de marea (TGP)[17],
expresado generalmente hasta un grado máximo,
|
|
(3) |
|
|
|
donde:
-
-
-
-
-
-
-
-
En la ecuación que define el argumento
astronómico, el orden del desarrollo en armónicos esféricos da origen a ondas
con distintos períodos (Tabla 2), asociados a la rotación de la Tierra:
-
-
-
-
A partir del grado de aproximación del
desarrollo es posible obtener distintas ondas que se clasifican según su
período, amplitud y fase.
Los coeficientes del TGP se representan
mediante catálogos. Éstos consisten en tablas de amplitudes, fases y
frecuencias para cada armónico del mismo. La precisión y exactitud de los catálogos
aumenta a medida que se extiende el desarrollo y que se analiza el potencial
para más cuerpos celestes. Los catálogos más actuales (por ejemplo, Hartmann y
Wenzel [1995a, b]) consideran el desarrollo del potencial de marea hasta
De esta manera, cada catálogo de mareas
tendrá asociado determinada cantidad de ondas y un grado máximo (Tabla 1;
modificada de Wenzel [1997a]).
|
Tabla 1 Catálogos
de marea. Modificada de Wenzel (1997a) |
||
|
Catálogo |
Número |
Grado máximo del desarrollo |
|
Doodson (1921) |
378 |
3 |
|
Cartwright y
Edden (1971, 1973) |
505 |
3 |
|
Büllesfeld
(1985) |
656 |
4 |
|
Tamura (1987) |
1 200 |
4 |
|
Xi (1987) |
2 934 |
4 |
|
Hartmann y
Wenzel (1995a, b) |
12 935 |
6 |
A
partir de los catálogos del potencial de mareas, es posible representar el TGP
y calcular cada una de las componentes la aceleración de marea (
|
|
(4) |
La señal de marea
La observación del fenómeno de mareas (o señal de marea) involucra no sólo la dinámica de los cuerpos celestes descripta anteriormente, sino también cómo la Tierra responde a las fuerzas de marea actuantes. La Figura 3 (modificada de Agnew [2007]) ilustra el origen de las fuerzas de marea y la respuesta de la Tierra.
Como
se ha mencionado en la sección anterior, la aceleración de mareas en un punto
de observación
En la realidad, la Tierra no es rígida y posee océanos, por lo que las fuerzas de marea actúan sobre el sistema Tierra, simbolizado en la Figura 3 como el rectángulo de línea punteada. Dentro del rectángulo tenemos la respuesta de la Tierra al efecto de mareas terrestres (ahora sobre una Tierra que no es rígida ni homogénea).
Además del efecto de marea terrestre, la
presencia de océanos da origen a un efecto adicional: las fuerzas de marea
generan variaciones en la distribución de masas de agua. Al colocar una masa de
agua sobre la superficie terrestre, ésta produce deformaciones llamadas efectos
de carga. Dado que la Tierra responde en forma elástica a estas deformaciones,
los períodos con los que se generan efectos de carga asociados a las mareas
oceánicas son coincidentes a los de las mareas terrestres, ya que las fuerzas
que las derivan tienen las mismas frecuencias. Es decir, los efectos de carga
producidos por mareas oceánicas contienen el mismo espectro de frecuencias que
las mareas terrestres pero distintas amplitudes y fases. Por lo tanto, este
efecto se superpone al de mareas terrestres y, dependiendo de la distancia de
la estación a la costa, la carga de la marea oceánica puede variar entre 1% y
10% de la marea terrestre (Hinderer et
al., 2007).
Por otra parte, la respuesta de la Tierra a las mareas terrestres y a la carga oceánica se ve también afectada por variaciones locales en las propiedades elásticas de la Tierra (simbolizado como Parámetros Locales en la Figura 3).
Los fenómenos de mareas terrestres y carga oceánica mareal involucran no sólo la dinámica de los cuerpos celestes y las fuerzas involucradas, sino también la respuesta de la Tierra a dichas fuerzas. Esta respuesta de la Tierra a dichas fuerzas puede ser descripta mediante números adimensionales que describen cómo ésta se deforma.
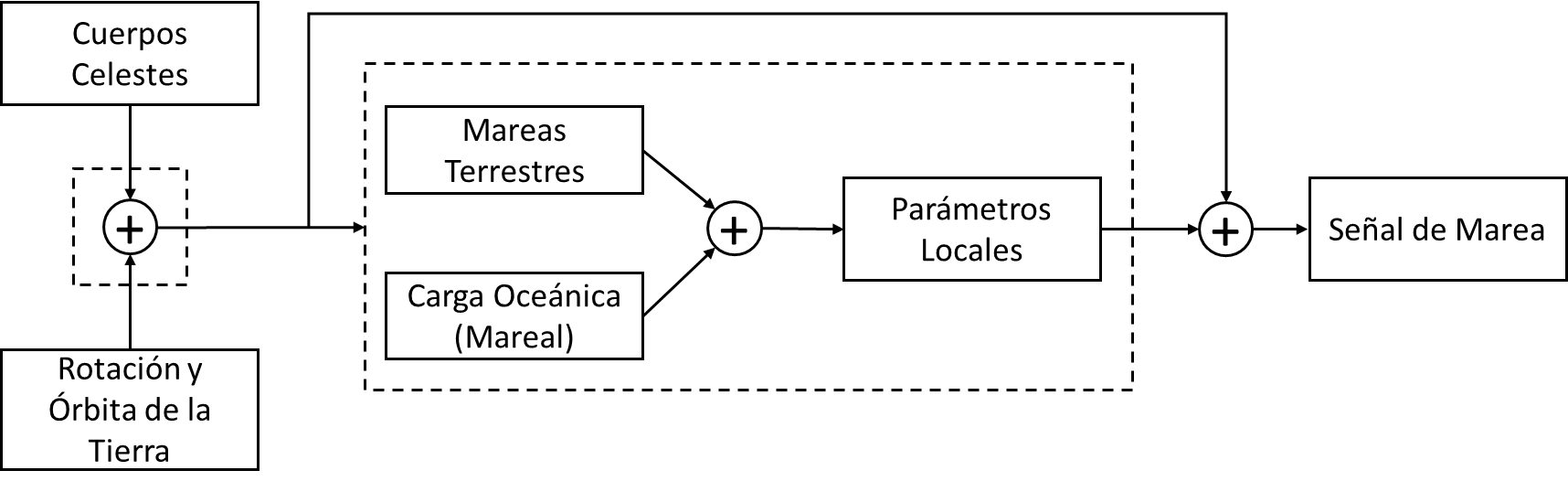
Figura 3. La señal de marea. Modificada de Agnew
(2007).
Estos números (llamados números de Love), fueron introducidos por Love en 1911, para un modelo de Tierra esférica y homogénea (Wang, 1997).
Modelos más complejos fueron publicados a lo largo del tiempo, sabiendo que la Tierra no es esférica, no es homogénea y rota (Wang, 1997). El modelo de Tierra más aceptado hoy en día y utilizado para realizar análisis de mareas es el propuesto por Dehant et al. (1999), el cual presenta los números de Love para una Tierra elipsóidica, anelástica y no-hidrostática. Este modelo es el utilizado en el desarrollo de este trabajo y nos referiremos a él como DDW-NHi.
|
Tabla 2 Principales ondas de marea y sus
amplitudes teóricas en AGGO |
|||||
|
Onda |
Grado |
Orden |
Período [días] |
Origen |
Amplitud Teórica [nm/s^2] |
|
Mm |
2 |
0 |
27.554 |
Luna |
5.1 |
|
Mf |
2 |
0 |
13.660 |
Luna |
1.5 |
|
Q1 |
2 |
1 |
1.120 |
Luna |
55.8 |
|
O1 |
2 |
1 |
1.076 |
Luna |
291.3 |
|
P1 |
2 |
1 |
1.003 |
Sol |
135.5 |
|
S1 |
2 |
1 |
1.000 |
Sol |
3.2 |
|
K1 |
2 |
1 |
0.997 |
Luna + Sol |
409.5 |
|
J1 |
2 |
1 |
0.962 |
Luna |
22.9 |
|
OO1 |
2 |
1 |
0.929 |
Luna |
12.5 |
|
2N2 |
2 |
2 |
0.538 |
Luna |
12.8 |
|
N2 |
2 |
2 |
0.527 |
Luna |
96.8 |
|
M2 |
2 |
2 |
0.517 |
Luna |
505.6 |
|
L2 |
2 |
2 |
0.508 |
Luna |
14.3 |
|
S2 |
2 |
2 |
0.500 |
Sol |
235.2 |
|
K2 |
2 |
2 |
0.499 |
Luna + Sol |
63.9 |
|
M3 |
3 |
3 |
0.345 |
Luna |
8.2 |
Dado el potencial de mareas, desarrollado por un determinado catálogo y un modelo de Tierra (conjunto de números de Love) es posible conocer la respuesta de la Tierra a las fuerzas de marea en cualquier punto de la misma. Dicha respuesta teórica (obtenida de modelos) difiere de la señal de marea observada ya que las propiedades elásticas reales de la Tierra difieren de las del modelo teórico, ya sea por deficiencias del modelo o por variaciones locales de las propiedades elásticas.
La Tabla 2 muestra la amplitud teórica de las principales ondas de marea, utilizando el modelo de Tierra DDW-NHi, propuesto por Dehant et al. (1999) y el catálogo de mareas de Hartmann y Wenzel (1995a, b), para la estación AGGO.
Análisis de marea
El principal objetivo a la hora de realizar un análisis de marea a partir de datos observados es conocer la respuesta del sistema Tierra-estación-sensor, a las fuerzas de marea; o bien conocer las desviaciones de dicha respuesta respecto de un modelo teórico (Wenzel, 1997b).
Hoy
en día, los análisis de marea y la determinación de parámetros de mareas se
realizan generalmente bajo el método de mínimos cuadrados. Dada la señal de
mareas observada (
La ecuación de observación puede ser descripta de
la siguiente manera (Schüller, 2019a):
|
|
(5) |
donde:
-
-
-
-
-
En la práctica,
|
|
(6) |
donde la Amplitud Observada es la amplitud
observada en la señal de marea del
Los softwares más clásicos para realizar
análisis de marea como el ETERNA 3.4 (Wenzel, 1996) o el BAYTAP-G (Tamura et al., 1991), permiten introducir
incógnitas adicionales (factores de regresión), asociadas a otros fenómenos
pero que tienen injerencia en la determinación de parámetros de marea (presión
atmosférica, efectos por movimiento del polo, entre otros), si estos no fueron
previamente eliminados de la señal a analizar.
|
|
(7) |
donde se
introducen <
En general, las observaciones de marea muestran
variaciones de muy largo período asociadas a efectos meteorológicos, hidrológicos
o a la deriva instrumental propia del instrumento en el caso de gravímetros
relativos. Éstas usualmente son tratadas de dos maneras:
· Filtrando la señal con un filtro pasa-altos antes de determinar los parámetros antes mencionados; o
· Introduciendo coeficientes de un polinomio de bajo grado en los parámetros a determinar en las Ecuación (7). En el caso del ETERNA, se introducen coeficientes de un polinomio de Chebychev, dada su estabilidad numérica (Schüller, 2019a). Éstas variaciones pueden ser escritas como (Wenzel, 1997b):
|
|
(8) |
donde
|
|
(9) |
El
grado del polinomio debe ser tal que no afecte la
determinación de los parámetros de marea y se determina en función de la
longitud de la serie temporal y el período máximo observado en la serie.
Si se agregan los coeficientes del
polinomio en la ecuación de observación (7), ésta queda de la forma:
|
|
(10) |
El sistema de ecuaciones dado por la
ecuación (10) es un sistema de ecuaciones no lineal respecto a las variables de
mayor interés:
|
|
(11) |
donde se
obtiene un sistema de ecuaciones lineal de la forma:
|
|
(12) |
Luego, el sistema de ecuaciones lineal dado
por la ecuación (12) puede escribirse en forma matricial como:
|
|
(13) |
donde
|
|
(14) |
Existen
tres razones para realizar el análisis de marea mediante el método de mínimos
cuadrados (Wenzel, 1997b):
I. El análisis por mínimos cuadrados puede ser aplicado a una serie observada, aún si esta presenta discontinuidades o períodos de tiempo sin datos.
II. Es posible obtener residuos y analizar el remanente de la señal, luego de eliminar la señal ajustada.
III.
Es posible determinar una
medida del error en la determinación de los parámetros ajustados (desvío
estándar), considerando también la propagación de
errores.
Metodología
En esta sección se describen los pasos seguidos para el acondicionamiento de la serie de datos observados por el SG038 y se describe el software utilizado para la determinación de los parámetros de marea.
Pre-procesamiento de
las observaciones
Previo a realizar un análisis de marea, debe realizarse un acondicionamiento de los datos del SG. Esto se realizó mediante el software TSOFT (Van Camp et al., 2005), tomando en cuenta las observaciones de tres años consecutivos (de enero de 2016 a diciembre de 2018) del SG038 instalado en AGGO. El pre-procesamiento de las observaciones consistió en los siguientes pasos, representados en la Figura 4:
I. Las observaciones del SG038 en voltaje con un intervalo de muestreo
de
Para obtener los residuos preliminares, se
modelaron los efectos principales (presión atmosférica, mareas terrestres,
carga oceánica y efecto del movimiento del polo) y se sustrajeron de la señal.
Los efectos atmosféricos se obtuvieron mediante el servicio de cálculo de
atracción atmosférica Atmacs[18] de
la BKG (Klügel y Wziontek, 2009) y el registro local de presión atmosférica para
mejorar la resolución temporal. La señal de marea teórica se calculó utilizando
el catálogo de Tamura (Tamura, 1987) y parámetros sintéticos para las
principales
ondas de marea del modelo DDW-NHi (Dehant et
al., 1999). El efecto de
carga oceánica se calculó utilizando el modelo FES2014b (Carrere et al., 2016) con parámetros
proporcionados por el Ocean Tide Loading
Provider http://holt.oso.chalmers.se/loading/; Bos y Scherneck, 2013). El efecto gravimétrico debido al
movimiento del polo se obtuvo a partir de la serie de coordenadas del polo EOP
C04 del Servicio Internacional de Rotación y Sistemas de Referencia de la Tierra (IERS),[19]
utilizando un factor de amplitud de 1.16 (Wahr, 1985).
Figura 4. a) Señal observada por el SG038, luego de aplicar el factor de calibración. b) Efecto de la presión atmosférica en AGGO. c) Señal de marea teórica (verde) y señal de carga oceánica del FES2014b (rojo). d) Efecto del movimiento del polo. e) Residuos preliminares (verde) y residuos luego del pre-procesamiento y filtrado (rojo). El efecto de deriva instrumental no fue eliminado.
II. Picos y pequeños gaps se eliminaron manualmente por interpolación lineal para tener una señal suave y sin perturbaciones. Un único salto fue encontrado en noviembre del año 2016, el cual fue generado por un corte en el suministro eléctrico. Éste fue corregido manualmente introduciendo un salto equivalente al observado (Figura 4e).
III. La señal se filtró con el propósito de eliminar señales cuyas frecuencias no contribuyen al modelo de marea. Se aplicó un filtro pasa bajos por mínimos cuadrados con una frecuencia de corte de 48 ciclos por día y un tamaño de ventana de 200 muestras, de forma tal que no existe pérdida de energía en el rango de frecuencias de mareas pero se elimina el ruido de alta frecuencia, generado principalmente por señales micro-sísmicas y por el propio ruido de la estación.
IV. Finalmente, se restauraron los efectos de la marea terrestre, carga oceánica y movimiento del polo eliminados en el paso II). La señal obtenida se decimó con un intervalo de muestreo de 1 hora para su posterior análisis de mareas.
Análisis de marea
El
análisis de marea de las observaciones, luego del pre-procesamiento, fue
realizado con el software ETERNA ETA34-X (Schüller, 2019a; Schüller, 2019b),
siendo este una actualización y extensión del clásico paquete ETERNA 3.4
(Wenzel, 1996). El retraso de tiempo de 8.3 segundos, causado por los componentes
electrónicos del SG038 fue tenido en cuenta (Antokoletz et al., 2017). Los efectos debidos al movimiento del polo y a la
longitud del día (LOD),[20] fueron
corregidos previo a realizar el ajuste por mínimos cuadrados de las distintas
componentes de marea.
La ecuación de observación tenida en
cuenta es similar a la de la Ecuación (12). En el caso de este trabajo no han
sido determinados factores de regresión ya que los principales efectos
(efectos atmosféricos y por movimiento del polo) que tienen impacto sobre la
determinación de los parámetros de marea fueron eliminados durante el
pre-procesamiento. El modelo de Tierra utilizado fue el DDW-NHi (Dehant et al., 1999) y el catálogo de mareas
propuesto por Hartmann y Wenzel (1995a y b), teniendo éste una precisión suficiente
respecto a la resolución del gravímetro superconductor (
Como resultado se obtuvieron factores de
amplitud y desfasajes para un conjunto de 55 grupos de onda, incluyendo ondas
de largo período, ondas diurnas y semi-
diurnas, pertenecientes al grado 2 del desarrollo en armónicos esféricos del
potencial de marea. Dentro del conjunto de ondas analizadas, se tuvieron en
cuenta también los órdenes 1 y 2 del grado 3 del potencial para aquellas ondas
de mayor amplitud en el área de estudio (O1, Q1, NO1, J1, N2, M2, S2 y K2). Por
último, las ondas M3 (grado 3 y orden 3 del potencial de marea) y M4 (grado 4 y
orden 4 del potencial de marea) también fueron analizadas. Respecto a las
variaciones y tendencias de largo período (como la deriva instrumental), dado
que éstas se comportan en forma lineal en el período de tiempo analizado, se
ajustó un polinomio de primer grado.
Los fenómenos de mareas terrestres y carga
oceánica, si bien son efectos con un mismo origen y frecuencias coincidentes,
es posible separarlos de dos formas:
· Teniendo en cuenta un modelo de Tierra sólida. De la señal de marea total observada es posible sustraer el modelo de mareas terrestres teórico y estudiar el residuo. Dicho residuo estará asociado al efecto de carga oceánica;
· Teniendo en cuenta un modelo de carga oceánica. Estos modelos están representados comúnmente por las principales componentes de marea (largo período, ondas diurnas y semi-diurnas). De la señal de marea total observada es posible sustraer el modelo de carga oceánica y estudiar las mareas terrestres o evaluar un modelo de Tierra.
El software ETERNA ETA34-X permite, dados
los parámetros de un modelo de carga oceánica, reducir los parámetros de marea
ajustados y obtener los correspondientes a las mareas terrestres. Esto permite
no solo evaluar el modelo de Tierra sino también analizar qué tan bien se ajusta
el modelo de carga oceánica a las observaciones en el área de estudio. Para este
trabajo, se tuvieron en cuenta cuatro modelos de marea oceánica y parámetros
proporcionados por el Ocean Tide Loading Provider (http://holt.oso.chalmers.se/loading/; Bos y Scherneck,
2013):
· EOT11a (Savcenko et al., 2012);
· FES2014b (Carrere et al., 2016);
· TPXO9-Atlas (Egbert y Erofeeva, 2002);
· GOT4.10c (Cheng y Andersen, 2010).
La Figura 5 muestra la relación vectorial entre los vectores observados, de carga oceánica y teórico. Es claro que el vector observado, una vez reducido por el efecto de carga oceánica debiera ser similar al vector de marea teórico si: (a) el modelo de carga oceánica es correcto; y/o (b) el modelo de Tierra considerado es correcto.
Los parámetros de las principales ondas de marea (Mm, Mf, Q1, O1, P1, K1, N2, M2, S2 y K2) fueron introducidos en el análisis a fin de estudiar el impacto de la carga oceánica en la estación AGGO y, además, comparar estos respecto de los parámetros teóricos del modelo de Tierra introducido.
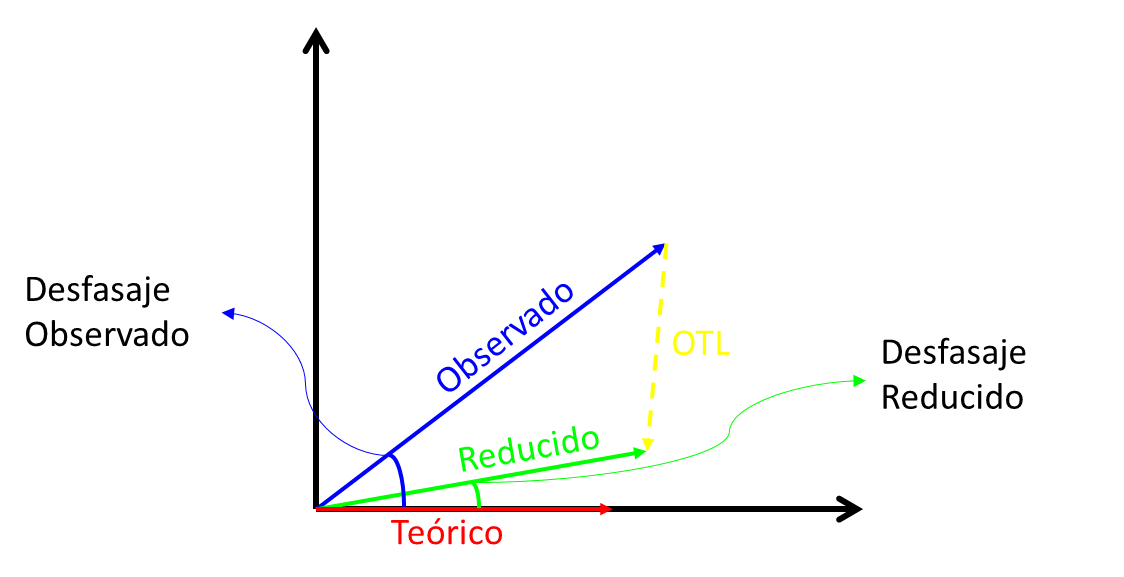
Figura 5. Relación entre los vectores observados, de carga oceánica (OTL[21]) y el teórico (derivado de un modelo de Tierra y un catálogo de mareas).
Resultados y análisis
Análisis de mareas
Factores de amplitud y desfasajes fueron determinados para un conjunto de 55 grupos de ondas de marea. Dichos resultados se presentan en la Tabla 3 para las principales ondas de marea que poseen mayor amplitud en la estación. En general, es de notar que para aquellas ondas que presentan mayor amplitud en la estación AGGO, los parámetros de marea (tanto factores de amplitud como desfasajes), son mejor determinados en el ajuste, presentando desvíos estándar más pequeños. A medida que la amplitud teórica de la onda analizada disminuye, resulta más difícil su determinación y, en consecuencia, los desvíos estándar son mayores.
En
el caso de las ondas mensuales y semi-mensuales (Mm y Mf, respectivamente) éstas
no son bien determinadas en el ajuste, presentando desvíos estándar altos,
respecto al parámetro estimado. Esto se debe a que las amplitudes de estas
ondas son débiles en las latitudes correspondientes a las de la estación AGGO (
et al., [2018]) pueden estar afectando la determinación de dichas ondas.
|
Tabla 3 Resultados del análisis
armónico para las principales ondas de marea |
|||||||
|
Onda |
Rango de frecuencias |
Amplitud teórica [nm/s^2] |
Factor de amplitud (H) |
Desvío |
Desfasaje [°] |
Desvío |
|
|
Desde |
Hasta |
||||||
|
Mm |
0.019700 |
0.050500 |
5.048 |
1.25145 |
0.4196 |
0.134 |
19.149 |
|
Mf |
0.053000 |
0.400000 |
1.527 |
1.81537 |
0.9959 |
7.220 |
31.466 |
|
Q1 |
0.879000 |
0.894500 |
55.772 |
1.19933 |
0.0017 |
0.110 |
0.079 |
|
O1 |
0.913900 |
0.932250 |
291.295 |
1.18837 |
0.0004 |
-0.163 |
0.018 |
|
NO1 |
0.965076 |
0.966757 |
22.898 |
1.17653 |
0.0037 |
-0.396 |
0.178 |
|
P1 |
0.996201 |
0.999674 |
135.517 |
1.17034 |
0.0003 |
-0.222 |
0.017 |
|
S1 |
0.999679 |
1.001663 |
3.202 |
1.42347 |
0.0203 |
-4.273 |
0.818 |
|
K1 |
1.001677 |
1.004115 |
409.514 |
1.15590 |
0.0002 |
-0.267 |
0.007 |
|
J1 |
1.036560 |
1.053060 |
22.906 |
1.16764 |
0.0044 |
-0.168 |
0.214 |
|
OO1 |
1.073160 |
1.096600 |
12.527 |
1.17093 |
0.0074 |
0.728 |
0.360 |
|
N2 |
1.878200 |
1.898429 |
96.802 |
1.19592 |
0.0003 |
0.920 |
0.015 |
|
M2 |
1.931400 |
1.933987 |
505.582 |
1.18166 |
0.0001 |
0.538 |
0.002 |
|
S2 |
1.997713 |
2.001215 |
235.202 |
1.16659 |
0.0002 |
0.135 |
0.007 |
|
K2 |
2.004395 |
2.030489 |
63.898 |
1.16461 |
0.0006 |
0.251 |
0.027 |
|
M3 |
2.885000 |
2.915496 |
8.150 |
1.08973 |
0.0013 |
0.841 |
0.071 |
|
M4 |
3.864500 |
3.864600 |
0.122 |
1.27095 |
0.0561 |
-7.274 |
2.530 |
|
Grado
3 del Potencial de Marea |
|||||||
|
Q1 |
0.879000 |
0.894500 |
0.973 |
1.30997 |
0.2470 |
3.098 |
10.800 |
|
O1 |
0.913900 |
0.932250 |
0.498 |
1.11176 |
0.2736 |
-10.118 |
14.100 |
|
NO1 |
0.965076 |
0.966757 |
3.045 |
1.30702 |
0.2215 |
-1.445 |
9.700 |
|
J1 |
1.036560 |
1.053060 |
1.111 |
1.30568 |
0.2438 |
-3.344 |
10.700 |
|
N2 |
1.878200 |
1.898429 |
7.036 |
1.08245 |
0.0051 |
-0.059 |
0.272 |
|
M2 |
1.931400 |
1.933987 |
1.061 |
1.12783 |
0.0269 |
1.082 |
1.368 |
|
S2 |
1.997713 |
2.001215 |
0.066 |
2.50240 |
0.5754 |
1.045 |
13.173 |
|
K2 |
2.004395 |
2.030489 |
0.354 |
0.99323 |
0.0908 |
-3.370 |
5.239 |
En
cuanto a las ondas diurnas y semi-diurnas, aquellas de mayor amplitud (como las
ondas Q1, O1, P1, K1, N2, M2, S2 y K2) son las mejor determinadas en el ajuste,
mostrando desvíos estándar más bajos, tanto para los factores de amplitud como
para las fases. Las ondas de menor amplitud, aún en el rango de frecuencias
diurnas y semi-diurnas, presentan desvíos estándar más significativos,
comparados al parámetro estimado. A fin de determinar en forma más precisa los
parámetros de marea de dichas ondas es necesario extender la longitud de la
serie de datos a analizar. Esto es también visible para la determinación de las
fases, donde las ondas de mayor amplitud presentan desfasajes mejor
determinados (desvíos estándar más bajos). Existen casos particulares, como la
onda NO1, cuyo factor de amplitud es mejor determinado que el desfasaje (en
comparación al parámetro estimado). Esto puede deberse a que la amplitud de la
onda es considerable pero, dado que esta onda ha sido incluida
también en el grado 3 del potencial, su separación en términos de desfasaje es
más difícil.
Respecto
a la onda terdiurna M3, ésta pudo ser bien separada en el ajuste por tener un
rango de frecuencias bien diferenciado de las ondas diurnas y semi-diurnas. M4,
por su parte, tiene una amplitud teórica pequeña en la estación (menor a
Si bien el grado 3 del potencial ha sido analizado para las principales ondas de marea, la determinación de las fases no es precisa. Esto se debe a que se trata de ondas de amplitudes débiles (comparadas a las descriptas previamente) y que la longitud de la serie de datos analizada no es suficientemente larga. Según Schüller (2019b), éstas ondas podrían ser bien determinadas contando como mínimo con 4.5 años de observaciones. Otro aspecto relacionado a la determinación de las ondas del grado 3 del potencial está asociado a que el rango de las frecuencias involucradas coincide con las correspondientes en el grado 2, por lo que su separación es más difícil. Cabe destacar que N2 tiene una amplitud teórica considerable, por lo que sería útil su determinación para generar un modelo de mareas preciso para la estación AGGO.
Los residuos del ajuste se presentan en la
Figura 6. El error medio cuadrático (RMS)[22] obtenido
a partir del procesamiento fue de
La Figura 7 muestra el espectro de
amplitud de los residuos. Si bien existe una importante contribución de efectos
de largo período (inferiores a 1 ciclo por día), los residuos no muestran
remanentes significativos de constituyentes de marea diurnos o semi-diurnos en
el espectro de amplitud.
Figura 6. Residuos obtenidos luego del ajuste de
los parámetros de marea.
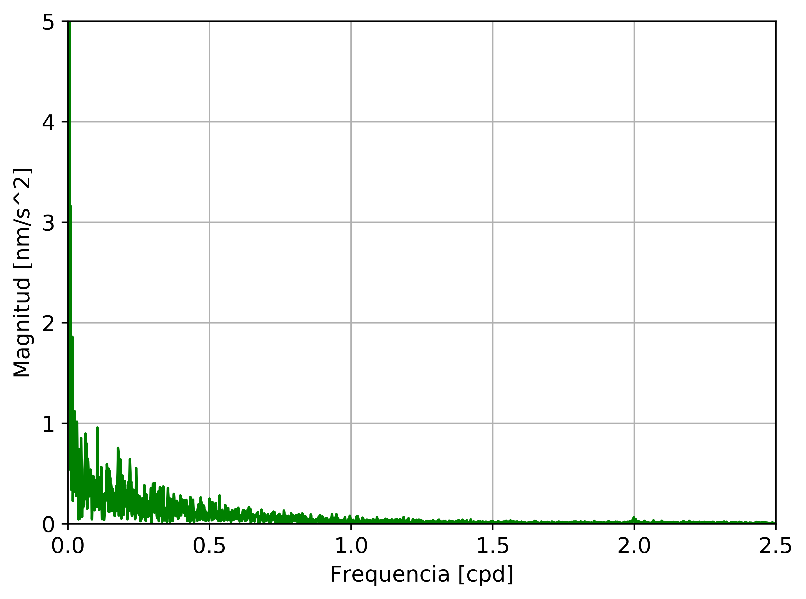
Figura 7. Espectro de amplitud de los residuos
obtenidos.
Carga oceánica
La Tabla 4
muestra los factores de amplitud teóricos derivados del catálogo de
Hartmann y Wenzel (1995a y b) y el modelo de Tierra DDW-NHi. Las columnas
siguientes corresponden a los factores de amplitud y desfasajes para las
principales ondas de marea una vez reducidos, teniendo en cuenta los modelos EOT11a,
FES2014b, TPXO9-Atlas y GOT4.10c.
Como
puede apreciarse, en general FES2014b y TPXO9-Atlas muestran un mejor acuerdo
con los valores teóricos. Las ondas Q1 y K2 para el modelo GOT4.10c muestran
una mayor diferencia respecto del resto, lo cual puede estar hablando de una
falta de exactitud de dicho modelo en las cercanías de AGGO. En cuanto a las
ondas de más largo período, Mm y Mf, estas muestran mayores diferencias
respecto a los
valores teóricos, probablemente debido a que no son bien determinadas en el
ajuste.
Tabla 4 Factores de Amplitud y Fases reducidos teniendo en cuenta los modelos |
||||||||||
|
Ondas |
Factor de Amplitud Teórico |
EOT11a |
FES2014b |
TPXO9-Atlas |
GOT4.10c |
|||||
|
Factor de Amplitud |
Fase |
Factor de Amplitud |
Fase |
Factor de Amplitud |
Fase |
Factor de Amplitud |
Fase |
|||
|
Mm |
1.07683 |
1.23658 |
-0.118 |
1.19172 |
-0.861 |
1.19893 |
-0.339 |
1.19996 |
0.183 |
|
|
Mf |
1.19994 |
1.33702 |
13.084 |
1.35349 |
13.997 |
1.38680 |
14.320 |
1.25360 |
13.989 |
|
|
Q1 |
1.15421 |
1.14986 |
0.066 |
1.15138 |
-0.037 |
1.15473 |
-0.242 |
1.17098 |
2.562 |
|
|
O1 |
1.15421 |
1.15460 |
0.099 |
1.15551 |
0.081 |
1.15328 |
-0.056 |
1.15351 |
0.034 |
|
|
P1 |
1.14920 |
1.15016 |
-0.114 |
1.15023 |
0.028 |
1.15117 |
-0.031 |
1.15040 |
0.045 |
|
|
K1 |
1.13515 |
1.13780 |
-0.018 |
1.13697 |
0.032 |
1.13794 |
0.007 |
1.13639 |
0.020 |
|
|
N2 |
1.16183 |
1.17192 |
0.061 |
1.16238 |
0.106 |
1.16121 |
0.143 |
1.16484 |
0.170 |
|
|
M2 |
1.16183 |
1.16412 |
-0.093 |
1.16199 |
0.050 |
1.16272 |
0.021 |
1.16170 |
0.010 |
|
|
S2 |
1.16183 |
1.15839 |
-0.182 |
1.16063 |
-0.118 |
1.16015 |
-0.105 |
1.15905 |
-0.041 |
|
|
K2 |
1.16183 |
1.16233 |
-0.094 |
1.16188 |
0.025 |
1.16112 |
-0.006 |
1.21401 |
-1.006 |
|
Estos resultados son ilustrados en la Figura 8. Las ondas Mm y Mf han sido excluidas del gráfico dado que no fueron bien determinadas en el análisis de marea y dificultan la interpretación de las ondas diurnas y semi-diurnas. En rojo se muestra el factor de amplitud teórico (el desfasaje es cero) y en azul el observado (luego del procesamiento), con sus respectivas barras de error. En gris, amarillo, celeste y verde se muestran las amplitudes y desfasajes obtenidos luego de reducir los parámetros observados con los modelos EOT11a, FES2014b, TPXO9-Atlas y GOT4.10c, respectivamente.
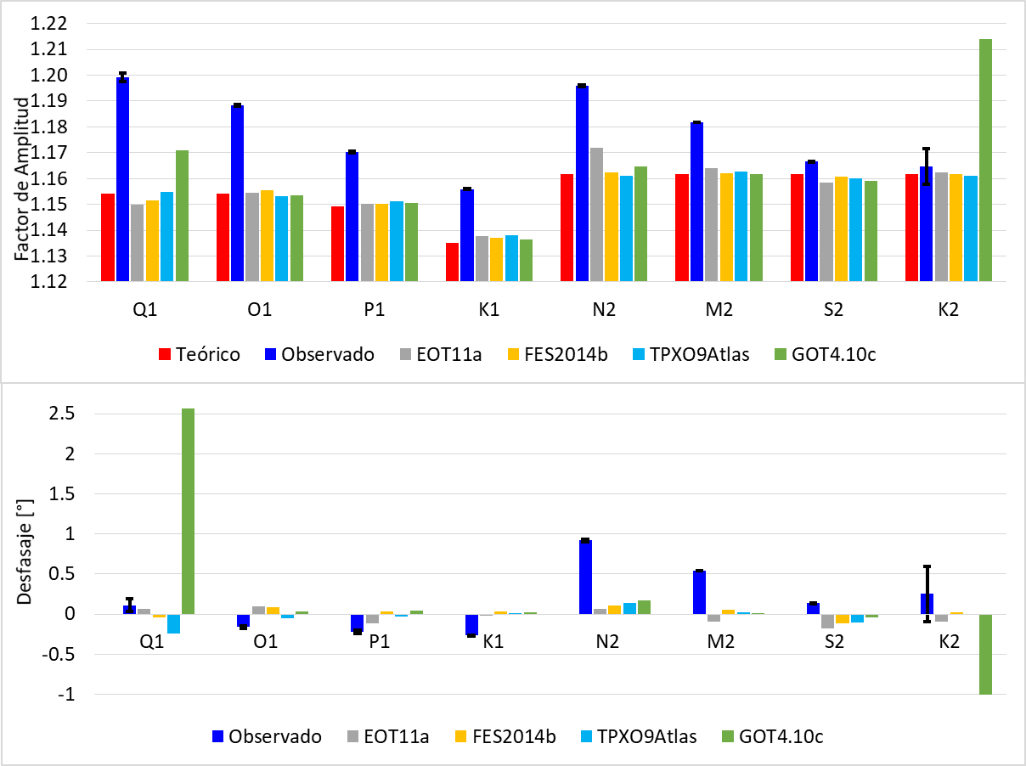
Figura 8. Análisis de las principales ondas de marea, luego de ser reducidas con distintos modelos de carga oceánica. Arriba: Factor de Amplitud. Abajo: Desfasaje. En el caso de los parámetros observados se muestran en negro las barras de error obtenidos del ajuste.
Conclusiones
Un modelo de mareas se presenta para la estación AGGO, a partir del análisis de tres años consecutivos (2016 a 2018) de observaciones gravimétricas realizadas con el gravímetro superconductor SG038. Dicho modelo incluye los efectos de mareas terrestres y carga oceánica. Los parámetros de marea (factores de amplitud y desfasajes) se ajustaron mediante el método de mínimos cuadrados para un total de 55 grupos de ondas. La última versión del software ETERNA ETA34-X ha sido utilizada para el análisis de marea. Además del grado 2 del potencial, los órdenes 1 y 2 del grado 3 del potencial de marea han sido incluidos para aquellas ondas de mayor amplitud en la estación. Las ondas diurnas y semi-diurnas han sido en general bien determinadas, mientras que para las ondas mensuales y semi-mensuales (Mm y Mf), la longitud de la serie de datos no resulta suficiente para determinarlas, siendo éstas de menor amplitud en la estación. Además, es posible que efectos de carácter no-mareal estén afectando la determinación de dichas ondas.
Los residuos del ajuste muestran un remanente de carácter no-mareal, principalmente asociado a efectos hidrológicos y efectos de carga no-mareal del océano. Esto será estudiado con mayor detalle en el futuro.
Se han analizado cuatro modelos de mareas oceánicas con el fin de separar los efectos de mareas terrestres y carga oceánica: EOT11a, FES2014b, TPXO9-Atlas y GOT4.10c. Los resultados obtenidos muestran un mejor acuerdo de los modelos FES2014b y TPXO9-Atlas con las observaciones. GOT4.10c muestra mayores diferencias para las ondas Q1 y K2 en amplitud y fase respecto del resto de los modelos. Sería de esperar que las correcciones de observables geodésicos en el área de trabajo generadas con estos modelos sean menos precisas. Las ondas Mm y Mf no están bien reducidas dado que no están correctamente determinadas en el análisis de marea. Estos resultados permiten concluir que, dado el buen acuerdo de las observaciones con los efectos de carga oceánica obtenidos del FES2014b y el TPXO9-Atlas, éstos podrían ser utilizados para corregir observables geodésicos VLBI, SLR o GNSS por el efecto de carga oceánica.
El modelo de mareas obtenido permite sustraer las componentes periódicas de la señal observada por el gravímetro superconductor con el fin de estudiar otros efectos de carácter no-mareal de menor amplitud. Además, los parámetros de marea obtenidos en el presente trabajo pueden ser utilizados para generar correcciones de marea precisas a aplicar en las observaciones del gravímetro absoluto instalado en AGGO.
Por último, los parámetros de marea una vez reducidos por el efecto de carga oceánica pueden ser empleados en forma regional para corregir observaciones gravimétricas, no necesariamente realizadas en AGGO.
Agradecimientos
Este trabajo fue posible gracias a los directores científicos de AGGO: Dr. Claudio Brunini y Dr. Hayo Hase. Los autores también agradecen a I. Nowak, A. M. Cassino, M. Häfner, A. Lothhammer y A. Pasquaré por la operación y el mantenimiento del gravímetro superconductor.
Las
series temporales de gravedad del SG están disponibles en: http://isdc.gfz-potsdam.de/.
Los
autores agradecen también a los dos revisores anónimos, quienes se han tomado
el tiempo de leer el trabajo y realizar aportes para su versión final.
Bibliografía
Agnew, D.C.
(2007). “Earth Tides”, in Treatise on
Geophysics: Geodesy, T.A. Herring (ed.), Elsevier, New York, 163-195.
Antokoletz,
E.D., Wziontek, H., Tocho, C. & Falk, R., in review. “Gravity reference at
the Argentinean-German Geodetic Observatory (AGGO) by co-location of
superconducting and absolute gravity measurements”, Journal of Geodesy.
Antokoletz,
E.D., Wziontek, H. & Tocho, C. (2017). “First six months of Superconducting
Gravimetry in Argentina”, in International Symposium on Gravity, Geoid and
Height Systems 2016, Springer, Cham, 111-118. https://doi.org/10.1007/1345_2017_13
Bos, M. &
Scherneck, H.G. (2013). “Computation of Green’s Functions for Ocean Tide
Loading”, in Xu G. (eds.), Sciences of
Geodesy – II, Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-28000-9_1
Büllesfeld, F.J.
(1985). Ein Beitrag zur harmonischen
Darstellung des gezeitenerzeugenden Potentials, Deutsche Geodaetische
Kommission Bayer. Akad. Wiss, 314.
Carrere, L.;
Lyard, F.; Cancet, M.; Guillot, A. & Picot, N. (2016). “FES 2014, a new
tidal model-Validation
results and perspectives for improvements”, in Proceedings of the ESA Living Planet Symposium.
Cartwright,
D.E. & Tayler, R.J. (1971). “New computations of the tide-generating
potential”, Geophysical Journal
International, 23(1), 45-73. https://doi.org/10.1111/j.1365-246X.1971.tb01803.x.
Cartwright,
D.E. & Edden, A.C. (1973). “Corrected tables of tidal harmonics”, Geophysical Journal International, 33(3), 253-264. https://doi.org/10.1111/j.1365-246X.1973.tb03420.x
Cimbaro, S.R.;
Lauría, E.A. & Piñón, D.A. (2009). “Adopción del Nuevo Marco de Referencia
Geodésico Nacional”, trabajo presentado por el Instituto Geográfico Militar,
Buenos Aires, Argentina.
Cheng, Y.
& Andersen, O.B. (2010). Improvement in global ocean tide
model in shallow water regions Poster, SV,
1-68.
Dehant V.;
Defraigne P, & Wahr J.M. (1999). “Tides for a convective Earth”, J. Geophys. Res., 104(B1): 1035-1058. https://doi.org/10.1029/1998JB900051
Doodson, A.T.
(1921). “The harmonic development of the tide-generating potential”, Proceedings of the Royal Society of London. Series
A, Containing Papers of a Mathematical and Physical Character, 100(704): 305-329. https://doi.org/10.1098/rspa.1921.0088
Egbert, G.D.
& Erofeeva, S.Y. (2002). “Efficient inverse modeling of barotropic ocean
tides”, Journal of Atmospheric and Oceanic Technology, 19(2): 183-204. https://doi.org/10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2
Furones, Á.M.,
Julián, A.B.A. & Devesa, J.P. (2003). “Correcciones por efecto de marea a
observables geodésicos y gravimétricos de alta precisión. Topografía y
cartografía”, Revista del Ilustre Colegio
Oficial de Ingenieros Técnicos en Topografía, 20(118): 56-64.
Hartmann, T.
& Wenzel, H.G. (1995a). “The HW95 tidal potential catalogue”. Geophysical
Research Letters, 22(24): 3553-3556.
https://doi.org/10.1029/95GL03324
Hartmann, T.
& Wenzel, H.G. (1995b).
“Catalogue HW95 on the tide generating potential”, Marées terrestres, 123: 9278-9301.
Hase, H.;
Böer, A.; Riepl, S.; Schlüter, W.; Cecioni, A.; Bataille, K.; Amthauer, E.;
Baradit, E.; Narváez, A. & Cifuentes, O. (2003). “The TIGO-Project”, in New technologies in VLBI, 306: 347. http://adsabs.harvard.edu/full/2003ASPC..306..347H
Heiskanen,
W.A. & Moritz, H. (1967). Physical Geodesy, W.H. Freeman and Co. San
Francisco.
Hinderer, J.;
Crossley, D. & Warburton, R.J. (2007). Superconducting
Gravimetry, Treatise on Geophysics, 2nd edition, 3: 59-115.
Klügel, T.
& Wziontek, H. (2009). “Correcting gravimeters and tiltmeters for
atmospheric mass attraction using operational weather models”, Journal of Geodynamics, 48(3-5): 204-210.
https://doi.org/10.1016/j.jog.2009.09.010
Mikolaj, M.; Güntner,
A.; Brunini, C.; Wziontek, H.; Gende, M.; Schröder, S.; Cassino, A.M.;
Pasquaré, A.; Reich, M.; Hartmann, A.; Oreiro, F.A.; Pendiuk, J.; Guarracino,
L. & Antokoletz, E.D. (2019). “Hydrometeorological and gravity signals at
the Argentine-German Geodetic Observatory (AGGO) in La Plata”, Earth Syst. Sci. Data, 11: 1501-1513. https://doi.org/10.5194/essd-11-1501-2019
Oreiro, F.A.;
Wziontek, H.; Fiore, M.M.E.; D’Onofrio, E.E. & Brunini, C. (2018). “Non-Tidal Ocean Loading Correction
for the Argentinean-German Geodetic Observatory Using an Empirical Model of
Storm Surge for the Río de la Plata”, Pure
& Applied Geophysics, 175(5). https://doi.org/10.1007/s00024-017-1651-6
Savcenko, R.;
Bosch, W.; Dettmering, D. & Seitz, F. (2012). “EOT11a - Global Empirical
Ocean Tide model from multi-mission satellite altimetry, with links to model
results. https://doi.org/10.1594/PANGAEA.834232. Supplement to: Savcenko, R., Bosch W.
(2012), EOT11a - Empirical Ocean Tide
Model from Multi-Mission Satellite Altimetry, Deutsches Geodätisches Forschungsinstitut
(DGFI), München, 89: 49.
Schüller, K.
(2019a). Installation Guide. Manual-03-ETA34-X-V71-Installation-Guide, Surin
2019. Recuperado de http://ggp.bkg.bund.de/eterna/
Schüller, K.
(2019b). User’s Guide. Manual-02-ET34-ANA-V71,
Surin 2019. Recuperado de http://ggp.bkg.bund.de/eterna/
Tamura, Y. (1987). “A harmonic development of the
tide-generating potential”, Bull. Inf. Marées
Terrestres, 99: 6813-6855.
Tamura, Y.; Sato, T.;
Ooe, M. & Ishiguro, M. (1991). “A procedure for
tidal analysis with a Bayesian information criterion”, Geophysical Journal International, 104(3): 507-516. https://doi.org/10.1111/j.1365-246X.1991.tb05697.x
Van Camp, M.
& Vauterin, P. (2005). “Tsoft: graphical and interactive software for the analysis of time
series and Earth tides”, Computers &
Geosciences, 31(5): 631-640. https://doi.org/10.1016/j.cageo.2004.11.015
Voigt, C.;
Förste, C.; Wziontek, H.; Crossley, D.; Meurers, B.; Pálinkáš, V.; Hinderer, J.;
Boy, J.-P.; Barriot, J.-P. & Sun, H. (2016). Report on the Data Base of the
International Geodynamics and Earth Tide Service (IGETS), (Scientific Technical
Report STR – Data; 16/08), Potsdam: GFZ German Research Centre for Geosciences.
http://doi.org/10.2312/GFZ.b103-16087
Wang, R.
(1997). “Tidal response of the solid Earth”, in Tidal phenomena, Springer, Berlin, Heidelberg, 27-57. https://doi.org/10.1007/BFb0011456
Wahr, J.
(1985). “Deformation induced by polar motion”, J. Geophys. Res., 90(B11): 9363-9368. https://doi.org/10.1029/JB090iB11p09363
Wenzel, H.G.
(1996). “The nanogal software: Earth tide data processing package ETERNA 3.30”,
Bull. Inf Mareés Terrestres, 124:
9425-9439.
Wenzel, H.G.
(1997a). “Analysis of Earth tide observations”, in Tidal
Phenomena, Springer, Berlin, Heidelberg, 59-75. https://doi.org/10.1007/BFb0011457
Wenzel, H.G. (1997b). Tide-generating potential for the Earth. In Tidal phenomena, Springer,
Berlin, Heidelberg, 9-26. https://doi.org/10.1007/BFb0011455
Wziontek, H.;
Wilmes, H. & Bonvalot, S. (2012). “AGrav: An International Database for
Absolute Gravity Measurements”, in Kenyon S., Pacino M., Marti U. (eds.), Geodesy for Planet Earth, International Association of Geodesy
Symposia, vol. 136, Springer, Berlin, Heidelberg.
https://doi.org/10.1007/978-3-642-20338-1_130
Wziontek, H.;
Wolf, P.; Häfner, M.; Hase, H.; Nowak, I.; Rülke, A.; Wilmes, H. & Brunini,
C. (2017). Superconducting Gravimeter
Data from AGGO/La Plata - Level 1, GFZ Data Services. http://doi.org/10.5880/igets.lp.l1.001
Xi, Q. (1987).
“A new complete development of the tide-generating potential for the epoch
J2000”, Bull. Inf. Marées Terrestres, 99: 6766-6812. Recuperado de http://www.geophy.cn/EN/Y1987/V30/I04/349